For objects lying in a plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

 (2-dimensional space), the separating axis theorem states that, given two convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 shapes, there exists a line onto which their projections will be separate if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

 they are not intersecting. A line for which the objects have disjoint projections is called a separating axis. An equivalent way of stating the theorem is to say that two convex shapes in the plane are not intersecting if and only if a line can be placed with one shape to one side of the line and the other shape to the other side. Such a separating line will be perpendicular to a separating axis.

For three-dimensional space, an axis can be found where the projection of two convex shapes can be separated if and only if they are not intersecting. In 3D, lines and planes are duals, and you can thus turn the separating axis theorem for 3D into the separating plane theorem. The general result in n dimensions

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 is called the separating hyperplane theorem. This theory is due to Hermann Minkowski

Hermann Minkowski

Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...

. The Hahn-Banach separation theorem generalizes the result to topological vector spaces.

A related result is the supporting hyperplane theorem.

Uniqueness

Separating axes are not unique, as any line parallel to a separating axis is also a separating axis. Further, if the convex sets are compact, they will be separated by a positive distance on a separating axis, and thus any line whose slope is close enough to the separating axis will also be a separating axis.

Separating lines may be unique, if the sets are distance 0 apart (properly, if there are points in each that are arbitrarily close to points in the other) – for instance, if one set is the open left half-plane  and the other is the open right half-plane 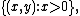then the y-axis  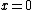is the only separating line. This can also hold for closed sets (if unbounded), if the sets are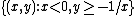


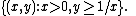
However, for compact sets, separating lines are not unique: non-intersecting compact sets are a positive distance apart, by applying the extreme value theorem

Extreme value theorem

In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...

 to the distance between points. Thus given a separating line between compact sets, a close enough parallel line will also be a separating line: visually, there is wiggle room.

Use in collision detection

The separating axis theorem says that if two convex objects are not penetrating, there exists an axis for which the projection of the objects will not overlap. This is an important definition because it suggests an algorithm for testing whether two convex solids intersect or not— in fact, it is heavily used in computational geometry, including computer games. It is also an important definition, because no matter what the dimensionality, the separating axis is always an axis — for example, in 3D, the space is separated by planes, but each plane is dual to a separating axis.

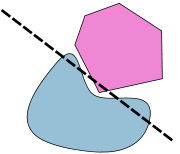
The separating axis theorem can be applied for fast collision detection

Collision detection

Collision detection typically refers to the computational problem of detecting the intersection of two or more objects. While the topic is most often associated with its use in video games and other physical simulations, it also has applications in robotics...

 between polygon meshes. Each face

Face (geometry)

In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

's normal

Surface normal

A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...

or other feature directions is used as a separating axis, as well as the cross products. Note that this yields possible separating axes, not separating lines/planes.

If the cross products were not used, certain edge-on-edge non-colliding cases would be treated as colliding. For increased efficiency, parallel axes may be calculated as a single axis.

External links

• Collision detection and response