Series-parallel networks problem
Encyclopedia
In combinatorial
mathematics
, the series-parallel networks problem asks for the number of series-parallel networks that can be formed using a given number of edges. The edges can be distinguishable or indistinguishable.
different networks on n edges.
By the duality of networks, it can be proved that the number of essentially series networks is equal to the number of essentially parallel networks. Thus for all n > 1, the number of networks in n edges is twice the number of essentially series networks. For n = 1, the number of networks is 1.
Define
Then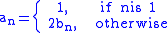
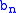can be found out by enumerating the partitions of 
.
Consider a partition,
of n:
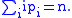
Consider the essentially series networks whose components correspond to the partition above. That is the number of components with i edges is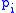
. The number of such networks can be computed as
Hence
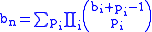
where the summation is over all partitions,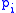
of n except for the trivial partition consisting of only n.
This gives a recurrence for computing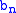
. Now 
can be computed as above.
[TODO: Generating function for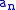
and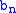 
are explained in the external links.]
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the series-parallel networks problem asks for the number of series-parallel networks that can be formed using a given number of edges. The edges can be distinguishable or indistinguishable.
Indistinguishable edges
When the edges are indistinguishable, we look for the number of topologicallyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
different networks on n edges.
Solution
The idea is to break-down the problem by classifying the networks as essentially series and essentially parallel networks.- An essentially series network is a network which can be broken down into two or more subnetworks in series.
- An essentially parallel network is a network which can be broken down into two or more subnetworks in parallel.
By the duality of networks, it can be proved that the number of essentially series networks is equal to the number of essentially parallel networks. Thus for all n > 1, the number of networks in n edges is twice the number of essentially series networks. For n = 1, the number of networks is 1.
Define
-
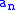as the number of series-parallel networks on n indistinguishable edges. -
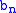as the number of essentially series networks.
Then
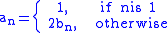
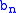can be found out by enumerating the partitions of .Consider a partition,
of n: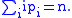Consider the essentially series networks whose components correspond to the partition above. That is the number of components with i edges is
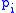. The number of such networks can be computed as
Hence
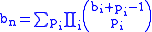
where the summation is over all partitions,
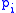of n except for the trivial partition consisting of only n.This gives a recurrence for computing
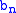. Now can be computed as above.[TODO: Generating function for
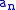and 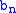are explained in the external links.]