Sethi-Ullman algorithm
Encyclopedia
In computer science
, the Sethi–Ullman algorithm is an algorithm
named after Ravi Sethi
and Jeffrey D. Ullman, its inventors, for translating abstract syntax tree
s into machine code
that uses as few instructions as possible.
has to decide which is the best way to translate the expression in terms of number of instructions used as well as number of registers needed to evaluate a certain subtree. Especially in the case that free registers are scarce, the order of evaluation can be important to the length of the generated code, because different orderings may lead to larger or smaller numbers of intermediate values being spilled
to memory and then restored. The Sethi–Ullman algorithm (also known as Sethi–Ullman numbering) fulfills the property of producing code which needs the least number of instructions possible as well as the least number of storage references (under the assumption that at the most commutativity
and associativity
apply to the operators used, but distributive laws i.e.
do not hold). Please note that the algorithm succeeds as well if neither commutativity
nor associativity
hold for the expressions used, and therefore arithmetic transformations can not be applied.
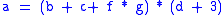, the abstract syntax tree
looks like this:
=
/ \
a *
/ \
/ \
+ +
/ \ / \
/ \ d 3
+ *
/ \ / \
b c f g
To continue with the algorithm, we need only to examine the arithmetic expression
, i.e. we only have to look at the right subtree of the assignment '=':
*
/ \
/ \
+ +
/ \ / \
/ \ d 3
+ *
/ \ / \
b c f g
Now we start traversing the tree (in preorder for now), assigning the number of registers needed to evaluate each subtree (note that the last summand in the expression
is a constant):
*2
/ \
/ \
+2 +1
/ \ / \
/ \ d1 30
+1 *1
/ \ / \
b1 c0f1 g0
From this tree it can be seen that we need 2 registers to compute the left subtree of the '*', but only 1 register to compute the right subtree. Nodes 'c' and 'g' do not need registers for the following reasons: If T is a tree leaf, then the number of registers to evaluate T is either 1 or 0 depending whether T is a left or a right subtree(since an operation such as add R1, A can handle the right component A directly without storing it into a register). Therefore we shall start to emit code for the left subtree first, because we might run into the situation that we only have 2 registers left to compute the whole expression. If we now computed the right subtree first (which needs only 1 register), we would then need a register to hold the result of the right subtree while computing the left subtree (which would still need 2 registers), therefore needing 3 registers concurrently. Computing the left subtree first needs 2 registers, but the result can be stored in 1, and since the right subtree needs only 1 register to compute, the evaluation of the expression can do with only 2 registers left.
Advanced Sethi–Ullman algorithm
See also
External links
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the Sethi–Ullman algorithm is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
named after Ravi Sethi
Ravi Sethi
Ravi Sethi is an Indian computer scientist retired from Bell Labs and president of Avaya Labs Research. He is best known as one of three authors of the classic computer science textbook Compilers: Principles, Techniques, and Tools, also known as the Dragon Book.Sethi was born in 1947 in Murdana,...
and Jeffrey D. Ullman, its inventors, for translating abstract syntax tree
Abstract syntax tree
In computer science, an abstract syntax tree , or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language. Each node of the tree denotes a construct occurring in the source code. The syntax is 'abstract' in the sense that it...
s into machine code
Machine code
Machine code or machine language is a system of impartible instructions executed directly by a computer's central processing unit. Each instruction performs a very specific task, typically either an operation on a unit of data Machine code or machine language is a system of impartible instructions...
that uses as few instructions as possible.
Overview
When generating code for arithmetic expressions, the compilerCompiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
has to decide which is the best way to translate the expression in terms of number of instructions used as well as number of registers needed to evaluate a certain subtree. Especially in the case that free registers are scarce, the order of evaluation can be important to the length of the generated code, because different orderings may lead to larger or smaller numbers of intermediate values being spilled
Register allocation
In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...
to memory and then restored. The Sethi–Ullman algorithm (also known as Sethi–Ullman numbering) fulfills the property of producing code which needs the least number of instructions possible as well as the least number of storage references (under the assumption that at the most commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
apply to the operators used, but distributive laws i.e.
do not hold). Please note that the algorithm succeeds as well if neither commutativityCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
nor associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
hold for the expressions used, and therefore arithmetic transformations can not be applied.
Simple Sethi–Ullman algorithm
The simple Sethi–Ullman algorithm works as follows (for a load-store architecture):- Traverse the abstract syntax treeAbstract syntax treeIn computer science, an abstract syntax tree , or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language. Each node of the tree denotes a construct occurring in the source code. The syntax is 'abstract' in the sense that it...
in pre- or postorder- For every non-constant leaf node, assign a 1 (i.e. 1 register is needed to hold the variable/field/etc.). For every constant leaf node (RHS of an operation – literals, values), assign a 0.
- For every non-leaf node n, assign the number of registers needed to evaluate the respective subtrees of n. If the number of registers needed in the left subtree (l) are not equal to the number of registers needed in the right subtree (r), the number of registers needed for the current node n is max(l, r). If l r, then the number of registers needed for the current node is l + 1.
- Code emission
- If the number of registers needed to compute the left subtree of node n is bigger than the number of registers for the right subtree, then the left subtree is evaluated first (since it may be possible that the one more register needed by the right subtree to save the result makes the left subtree spill). If the right subtree needs more registers than the left subtree, the right subtree is evaluated first accordingly. If both subtrees need equal as much registers, then the order of evaluation is irrelevant.
Example
For an arithmetic expression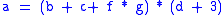, the abstract syntax treeAbstract syntax tree
In computer science, an abstract syntax tree , or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language. Each node of the tree denotes a construct occurring in the source code. The syntax is 'abstract' in the sense that it...
looks like this:
=
/ \
a *
/ \
/ \
+ +
/ \ / \
/ \ d 3
+ *
/ \ / \
b c f g
To continue with the algorithm, we need only to examine the arithmetic expression
, i.e. we only have to look at the right subtree of the assignment '=':*
/ \
/ \
+ +
/ \ / \
/ \ d 3
+ *
/ \ / \
b c f g
Now we start traversing the tree (in preorder for now), assigning the number of registers needed to evaluate each subtree (note that the last summand in the expression
is a constant):*2
/ \
/ \
+2 +1
/ \ / \
/ \ d1 30
+1 *1
/ \ / \
b1 c0f1 g0
From this tree it can be seen that we need 2 registers to compute the left subtree of the '*', but only 1 register to compute the right subtree. Nodes 'c' and 'g' do not need registers for the following reasons: If T is a tree leaf, then the number of registers to evaluate T is either 1 or 0 depending whether T is a left or a right subtree(since an operation such as add R1, A can handle the right component A directly without storing it into a register). Therefore we shall start to emit code for the left subtree first, because we might run into the situation that we only have 2 registers left to compute the whole expression. If we now computed the right subtree first (which needs only 1 register), we would then need a register to hold the result of the right subtree while computing the left subtree (which would still need 2 registers), therefore needing 3 registers concurrently. Computing the left subtree first needs 2 registers, but the result can be stored in 1, and since the right subtree needs only 1 register to compute, the evaluation of the expression can do with only 2 registers left.
Advanced Sethi–Ullman algorithm
In an advanced version of the Sethi–Ullman algorithm, the arithmetic expressions are first transformed, exploiting the algebraic properties of the operators used.
See also
- Strahler numberStrahler numberIn mathematics, the Strahler number or Horton–Strahler number of a mathematical tree is a numerical measure of its branching complexity....
, the minimum number of registers needed to evaluate an expression without any external storage
External links
Strahler number
In mathematics, the Strahler number or Horton–Strahler number of a mathematical tree is a numerical measure of its branching complexity....
, the minimum number of registers needed to evaluate an expression without any external storage