
Sextic equation
Encyclopedia
In mathematics
, a sextic equation is a polynomial
equation
of degree
six. It is of the form:
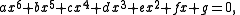
where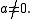
The coefficients a, b, c, d, e, f, g are members of a field
, (typically the rational number
s, the real number
s or the complex number
s), and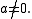
Because they have an even degree, normal sextic functions appear similar to normal quartic function
s when graphed, except they may possess an additional local maximum
and local minimum each. The derivative
of a sextic function is a quintic function.
Since a sextic function is a polynomial with even degree, it has the same limit when the argument goes to positive or negative infinity
. If a is positive, then the function increases to positive infinity at both sides; and thus the function has a global minimum. Likewise, if a is negative, it decreases to negative infinity and has a global maximum.
Another name for a sextic equation is a hexic equation.
developed techniques for determining whether a given equation could be solved by radicals which gave rise to the field of Galois theory
.
It follows from Galois theory that a sextic equation is solvable in term of radicals if and only if its Galois group
is contained either in the group of order 48 which permutes the roots as the isometries of a regular octahedron permute its vertices or in the group of order 72 which stabilizes a partition of the set of the roots into two subsets of three roots.
There are formulas to test either case, and, if the equation is solvable, compute the roots in term of radicals.
The general sextic equation can be solved in terms of Kampé de Fériet functions
. A more restricted class of sextics can be solved in terms of generalised hypergeometric functions in one variable using Felix Klein
's approach to solving the quintic equation
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sextic equation is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
of degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
six. It is of the form:
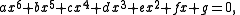
where
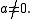
The coefficients a, b, c, d, e, f, g are members of a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, (typically the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), and
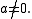
Because they have an even degree, normal sextic functions appear similar to normal quartic function
Quartic function
In mathematics, a quartic function, or equation of the fourth degree, is a function of the formf=ax^4+bx^3+cx^2+dx+e \,where a is nonzero; or in other words, a polynomial of degree four...
s when graphed, except they may possess an additional local maximum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
and local minimum each. The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a sextic function is a quintic function.
Since a sextic function is a polynomial with even degree, it has the same limit when the argument goes to positive or negative infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
. If a is positive, then the function increases to positive infinity at both sides; and thus the function has a global minimum. Likewise, if a is negative, it decreases to negative infinity and has a global maximum.
Another name for a sextic equation is a hexic equation.
Solvable sextics
Some sixth degree equations can be solved by factorizing into radicals, but other sextics cannot. Évariste GaloisÉvariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
developed techniques for determining whether a given equation could be solved by radicals which gave rise to the field of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
.
It follows from Galois theory that a sextic equation is solvable in term of radicals if and only if its Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
is contained either in the group of order 48 which permutes the roots as the isometries of a regular octahedron permute its vertices or in the group of order 72 which stabilizes a partition of the set of the roots into two subsets of three roots.
There are formulas to test either case, and, if the equation is solvable, compute the roots in term of radicals.
The general sextic equation can be solved in terms of Kampé de Fériet functions
Joseph Kampé de Fériet
Marie-Joseph Kampé de Fériet was professor at Université Lille Nord de France from 1919 to 1969...
. A more restricted class of sextics can be solved in terms of generalised hypergeometric functions in one variable using Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's approach to solving the quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
.

