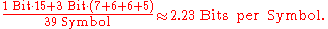Shannon–Fano coding
Encyclopedia
In the field of data compression
, Shannon–Fano coding, named after Claude Elwood Shannon
and Robert Fano
, is a technique for constructing a prefix code
based on a set of symbols and their probabilities (estimated or measured). It is suboptimal
in the sense that it does not achieve the lowest possible expected code word length like Huffman coding
; however unlike Huffman coding, it does guarantee that all code word lengths are within one bit of their theoretical ideal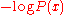
. The technique was proposed in Shannon's "A Mathematical Theory of Communication
", his 1948 article introducing the field of information theory
. The method was attributed to Fano, who later published it as a technical report
.
Shannon–Fano coding should not be confused with Shannon coding, the coding method used to prove Shannon's noiseless coding theorem, or with Shannon–Fano–Elias coding
(also known as Elias coding), the precursor to arithmetic coding
.
In Shannon–Fano coding, the symbols are arranged in order from most probable to least probable, and then divided into two sets whose total probabilities are as close as possible to being equal. All symbols then have the first digits of their codes assigned; symbols in the first set receive "0" and symbols in the second set receive "1". As long as any sets with more than one member remain, the same process is repeated on those sets, to determine successive digits of their codes. When a set has been reduced to one symbol, of course, this means the symbol's code is complete and will not form the prefix of any other symbol's code.
The algorithm works, and it produces fairly efficient variable-length encodings; when the two smaller sets produced by a partitioning are in fact of equal probability, the one bit of information used to distinguish them is used most efficiently. Unfortunately, Shannon–Fano does not always produce optimal prefix codes; the set of probabilities {0.35, 0.17, 0.17, 0.16, 0.15} is an example of one that will be assigned non-optimal codes by Shannon–Fano coding.
For this reason, Shannon–Fano is almost never used; Huffman coding
is almost as computationally simple and produces prefix codes that always achieve the lowest expected code word length, under the constraints that each symbol is represented by a code formed of an integral number of bits. This is a constraint that is often unneeded, since the codes will be packed end-to-end in long sequences. If we consider groups of codes at a time, symbol-by-symbol Huffman coding is only optimal if the probabilities of the symbols are independent
and are some power of a half, i.e.,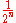
. In most situations, arithmetic coding
can produce greater overall compression than either Huffman or Shannon–Fano, since it can encode in fractional numbers of bits which more closely approximate the actual information content of the symbol. However, arithmetic coding has not superseded Huffman the way that Huffman supersedes Shannon–Fano, both because arithmetic coding is more computationally expensive and because it is covered by multiple patents.
Shannon–Fano coding is used in the IMPLODE compression method, which is part of the ZIP file format
.
All symbols are sorted by frequency, from left to right (shown in Figure a). Putting the dividing line between symbols B and C results in a total of 22 in the left group and a total of 17 in the right group. This minimizes the difference in totals between the two groups.
With this division, A and B will each have a code that starts with a 0 bit, and the C, D, and E codes will all start with a 1, as shown in Figure b. Subsequently, the left half of the tree gets a new division between A and B, which puts A on a leaf with code 00 and B on a leaf with code 01.
After four division procedures, a tree of codes results. In the final tree, the three symbols with the highest frequencies have all been assigned 2-bit codes, and two symbols with lower counts have 3-bit codes as shown table below:
Results in 2 bits for A, B and C and per 3 bits for D and E an average bit number of
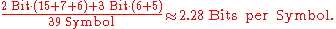
gave a different algorithm that always produces an optimal tree for any given probabilities. While the Shannon–Fano tree is created from the root to the leaves, the Huffman algorithm works from leaves to the root in the opposite direction.
In this case D & E have the lowest frequencies and so are allocated 0 and 1 respectively and grouped together with a combined probability of 0.28205128. The lowest pair now are B and C so they're allocated 0 and 1 and grouped together with a combined probability of 0.33333333. This leaves BC and DE now with the lowest probabilities so 0 and 1 are prepended to their codes and they are combined. This then leaves just A and BCDE, which have 0 and 1 prepended respectively and are then combined. This leaves us with a single node and our algorithm is complete.
The code lengths for the different characters this time are 1 bit for A and 3 bits for all other characters.
Results in 1 bit for A and per 3 bits for B, C, D and E an average bit number of
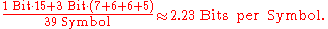
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, Shannon–Fano coding, named after Claude Elwood Shannon
Claude Elwood Shannon
Claude Elwood Shannon was an American mathematician, electronic engineer, and cryptographer known as "the father of information theory"....
and Robert Fano
Robert Fano
Robert Mario Fano is an Italian-American computer scientist, currently professor emeritus of Electrical Engineering and Computer Science at Massachusetts Institute of Technology. Fano is known principally for his work on information theory, inventing Shannon-Fano coding...
, is a technique for constructing a prefix code
Prefix code
A prefix code is a type of code system distinguished by its possession of the "prefix property"; which states that there is no valid code word in the system that is a prefix of any other valid code word in the set...
based on a set of symbols and their probabilities (estimated or measured). It is suboptimal
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
in the sense that it does not achieve the lowest possible expected code word length like Huffman coding
Huffman coding
In computer science and information theory, Huffman coding is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol where the variable-length code table has been derived in a particular way based on...
; however unlike Huffman coding, it does guarantee that all code word lengths are within one bit of their theoretical ideal
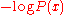. The technique was proposed in Shannon's "A Mathematical Theory of CommunicationA Mathematical Theory of Communication
"A Mathematical Theory of Communication" is an influential 1948 article by mathematician Claude E. Shannon. As of November 2011, Google Scholar has listed more than 48,000 unique citations of the article and the later-published book version...
", his 1948 article introducing the field of information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. The method was attributed to Fano, who later published it as a technical report
Technical report
A technical report is a document that describes the process, progress, or results of technical or scientific research or the state of a technical or scientific research problem. It might also include recommendations and conclusions of the research...
.
Shannon–Fano coding should not be confused with Shannon coding, the coding method used to prove Shannon's noiseless coding theorem, or with Shannon–Fano–Elias coding
Shannon–Fano–Elias coding
In information theory, Shannon–Fano–Elias coding is a precursor to arithmetic coding, in which probabilities are used to determine codewords....
(also known as Elias coding), the precursor to arithmetic coding
Arithmetic coding
Arithmetic coding is a form of variable-length entropy encoding used in lossless data compression. Normally, a string of characters such as the words "hello there" is represented using a fixed number of bits per character, as in the ASCII code...
.
In Shannon–Fano coding, the symbols are arranged in order from most probable to least probable, and then divided into two sets whose total probabilities are as close as possible to being equal. All symbols then have the first digits of their codes assigned; symbols in the first set receive "0" and symbols in the second set receive "1". As long as any sets with more than one member remain, the same process is repeated on those sets, to determine successive digits of their codes. When a set has been reduced to one symbol, of course, this means the symbol's code is complete and will not form the prefix of any other symbol's code.
The algorithm works, and it produces fairly efficient variable-length encodings; when the two smaller sets produced by a partitioning are in fact of equal probability, the one bit of information used to distinguish them is used most efficiently. Unfortunately, Shannon–Fano does not always produce optimal prefix codes; the set of probabilities {0.35, 0.17, 0.17, 0.16, 0.15} is an example of one that will be assigned non-optimal codes by Shannon–Fano coding.
For this reason, Shannon–Fano is almost never used; Huffman coding
Huffman coding
In computer science and information theory, Huffman coding is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol where the variable-length code table has been derived in a particular way based on...
is almost as computationally simple and produces prefix codes that always achieve the lowest expected code word length, under the constraints that each symbol is represented by a code formed of an integral number of bits. This is a constraint that is often unneeded, since the codes will be packed end-to-end in long sequences. If we consider groups of codes at a time, symbol-by-symbol Huffman coding is only optimal if the probabilities of the symbols are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
and are some power of a half, i.e.,
. In most situations, arithmetic codingArithmetic coding
Arithmetic coding is a form of variable-length entropy encoding used in lossless data compression. Normally, a string of characters such as the words "hello there" is represented using a fixed number of bits per character, as in the ASCII code...
can produce greater overall compression than either Huffman or Shannon–Fano, since it can encode in fractional numbers of bits which more closely approximate the actual information content of the symbol. However, arithmetic coding has not superseded Huffman the way that Huffman supersedes Shannon–Fano, both because arithmetic coding is more computationally expensive and because it is covered by multiple patents.
Shannon–Fano coding is used in the IMPLODE compression method, which is part of the ZIP file format
ZIP (file format)
Zip is a file format used for data compression and archiving. A zip file contains one or more files that have been compressed, to reduce file size, or stored as is...
.
Shannon–Fano Algorithm
A Shannon–Fano tree is built according to a specification designed to define an effective code table. The actual algorithm is simple:- For a given list of symbols, develop a corresponding list of probabilities or frequency counts so that each symbol’s relative frequency of occurrence is known.
- Sort the lists of symbols according to frequency, with the most frequently occurring symbols at the left and the least common at the right.
- Divide the list into two parts, with the total frequency counts of the left half being as close to the total of the right as possible.
- The left half of the list is assigned the binary digit 0, and the right half is assigned the digit 1. This means that the codes for the symbols in the first half will all start with 0, and the codes in the second half will all start with 1.
- Recursively apply the steps 3 and 4 to each of the two halves, subdividing groups and adding bits to the codes until each symbol has become a corresponding code leaf on the tree.
Example
The example shows the construction of the Shannon code for a small alphabet. The five symbols which can be coded have the following frequency:| Symbol | A | B | C | D | E |
|---|---|---|---|---|---|
| Count | 15 | 7 | 6 | 6 | 5 |
| Probabilities | 0.38461538 | 0.17948718 | 0.15384615 | 0.15384615 | 0.12820513 |
All symbols are sorted by frequency, from left to right (shown in Figure a). Putting the dividing line between symbols B and C results in a total of 22 in the left group and a total of 17 in the right group. This minimizes the difference in totals between the two groups.
With this division, A and B will each have a code that starts with a 0 bit, and the C, D, and E codes will all start with a 1, as shown in Figure b. Subsequently, the left half of the tree gets a new division between A and B, which puts A on a leaf with code 00 and B on a leaf with code 01.
After four division procedures, a tree of codes results. In the final tree, the three symbols with the highest frequencies have all been assigned 2-bit codes, and two symbols with lower counts have 3-bit codes as shown table below:
| Symbol | A | B | C | D | E |
|---|---|---|---|---|---|
| Code | 00 | 01 | 10 | 110 | 111 |
Results in 2 bits for A, B and C and per 3 bits for D and E an average bit number of
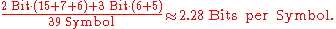
Huffman Algorithm
The Shannon–Fano algorithm doesn't always generate an optimal code. In 1952, David A. HuffmanDavid A. Huffman
David Albert Huffman was a pioneer in computer science. He is well-known for his Huffman coding. David Huffman died at the age of 74 after a 10-month battle with cancer.-Education:...
gave a different algorithm that always produces an optimal tree for any given probabilities. While the Shannon–Fano tree is created from the root to the leaves, the Huffman algorithm works from leaves to the root in the opposite direction.
- Create a leaf node for each symbol and add it to frequency of occurrence.
- While there is more than one node in the queue:
- Remove the two nodes of lowest probability or frequency from the queue
- Prepend 0 and 1 respectively to any code already assigned to these nodes
- Create a new internal node with these two nodes as children and with probability equal to the sum of the two nodes' probabilities.
- Add the new node to the queue.
- The remaining node is the root node and the tree is complete.
Example
Using the same frequencies as for the Shannon–Fano example above, viz:| Symbol | A | B | C | D | E |
|---|---|---|---|---|---|
| Count | 15 | 7 | 6 | 6 | 5 |
| Probabilities | 0.38461538 | 0.17948718 | 0.15384615 | 0.15384615 | 0.12820513 |
In this case D & E have the lowest frequencies and so are allocated 0 and 1 respectively and grouped together with a combined probability of 0.28205128. The lowest pair now are B and C so they're allocated 0 and 1 and grouped together with a combined probability of 0.33333333. This leaves BC and DE now with the lowest probabilities so 0 and 1 are prepended to their codes and they are combined. This then leaves just A and BCDE, which have 0 and 1 prepended respectively and are then combined. This leaves us with a single node and our algorithm is complete.
The code lengths for the different characters this time are 1 bit for A and 3 bits for all other characters.
| Symbol | A | B | C | D | E |
|---|---|---|---|---|---|
| Code | 0 | 100 | 101 | 110 | 111 |
Results in 1 bit for A and per 3 bits for B, C, D and E an average bit number of