Shear matrix
Encyclopedia
In mathematics
, a shear matrix or transvection is an elementary matrix that represents the addition of a multiple of one row or column to another. Such a matrix may be derived by taking the identity matrix
and replacing one of the zero elements with a non-zero value.
A typical shear matrix is shown below:
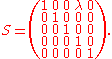
The name shear reflects the fact that the matrix represents a shear transformation. Geometrically, such a transformation takes pairs of points in a linear space, that are purely axially separated along the axis whose row in the matrix contains the shear element, and effectively replaces those pairs by pairs whose separation is no longer purely axial but has two vector components. Thus, the shear axis is always an eigenvector of S.
A shear parallel to the x axis results in x' = x +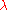
y and y' = y. In matrix form:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a shear matrix or transvection is an elementary matrix that represents the addition of a multiple of one row or column to another. Such a matrix may be derived by taking the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and replacing one of the zero elements with a non-zero value.
A typical shear matrix is shown below:
The name shear reflects the fact that the matrix represents a shear transformation. Geometrically, such a transformation takes pairs of points in a linear space, that are purely axially separated along the axis whose row in the matrix contains the shear element, and effectively replaces those pairs by pairs whose separation is no longer purely axial but has two vector components. Thus, the shear axis is always an eigenvector of S.
A shear parallel to the x axis results in x' = x +
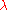y and y' = y. In matrix form:-
Similarly, a shear parallel to the y axis has x' = x and y' = y +
x. In matrix form:
-
Clearly the determinant will always be 1, as no matter where the shear element is placed, it will be a member of a skew-diagonal that also contains zero elements (as all skew-diagonals have length at least two) hence its product will remain zero and won't contribute to the determinant. Thus every shear matrix has an inverse, and the inverse is simply a shear matrix with the shear element negated, representing a shear transformation in the opposite direction. In fact, this is part of an easily derived more general result: if S is a shear matrix with shear element
, then Sn is a shear matrix whose shear element is simply n
. Hence, raising a shear matrix to a power n multiplies its shear factor by n.
Properties
If S is an n×n shear matrix, then:- S has rank n and therefore is invertible
- 1 is the only eigenvalue of S, so det S = 1 and trace S = n
- the eigenspace of S has n-1 dimensions.
- S is asymmetric
- S may be made into a block matrixBlock matrixIn the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
by at most 1 column interchange and 1 row interchange operation - the area, volume, or any higher order interior capacity of a polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
is invariant under the shear transformation of the polytope's vertices.
See also
- Linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
- Shear mapping
- Transformation matrix
- Elementary row operationsElementary row operationsIn mathematics, an elementary matrix is a simple matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices...
-