
Shift matrix
Encyclopedia
In mathematics
, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix.
The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix. The (i,j):th component of U and L are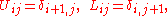
where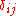 is the Kronecker delta symbol.
is the Kronecker delta symbol.
For example, the 5×5 shift matrices are
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix.
The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix. The (i,j):th component of U and L are
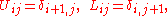
where
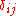 is the Kronecker delta symbol.
is the Kronecker delta symbol.For example, the 5×5 shift matrices are
-

Clearly, the transpose of a lower shift matrix is an upper shift matrix and vice versa.
Premultiplying a matrix A by a lower shift matrix results in the elements of A being shifted downward by one position, with zeroes appearing in the top row. Postmultiplication by a lower shift matrix results in a shift left.
Similar operations involving an upper shift matrix result in the opposite shift.
Clearly all shift matrices are nilpotentNilpotentIn mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n.
Properties
Let L and U be the n by n lower and upper shift matrices, respectively. The following properties hold for both U and L.
Let us therefore only list the properties for U:- detDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
(U) = 0 - traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
(U) = 0 - rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
(U) = n−1 - The characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
s of U is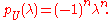
- Un = 0. This follows from the previous property by the Cayley–Hamilton theoremCayley–Hamilton theoremIn linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
.
- The permanentPermanentThe permanent of a square matrix in linear algebra, is a function of the matrix similar to the determinant. The permanent, as well as the determinant, is a polynomial in the entries of the matrix...
of U is 0.
The following properties show how U and L are related:- LT = U; UT = L
- The null spaceNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
s of U and L are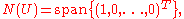
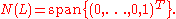
- The spectrumSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
of U and L is . The algebraic multiplicity of 0 is n, and its geometric multiplicity is 1. From the expressions for the null spaces, it follows that (up to a scaling) the only eigenvector for U is
. The algebraic multiplicity of 0 is n, and its geometric multiplicity is 1. From the expressions for the null spaces, it follows that (up to a scaling) the only eigenvector for U is  , and the only eigenvector for L is
, and the only eigenvector for L is 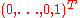 .
.
- For LU and UL we have
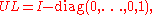
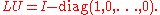
- These matrices are both idempotent, symmetric, and have the same rank as U and L
- Ln-aUn-a + LaUa = Un-aLn-a + UaLa = I (the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
), for any integer a between 0 and n inclusive.
Examples
-

Then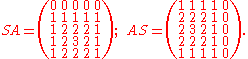
Clearly there are many possible permutations. For example,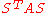 is equal to the matrix A shifted up and left along the main diagonal.
is equal to the matrix A shifted up and left along the main diagonal.
-
- det


