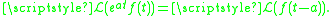Shift theorem
Encyclopedia
In mathematics
, the (exponential) shift theorem is a theorem
about polynomial
differential operators (D-operators) and exponential function
s. It permits one to eliminate, in certain cases, the exponential from under the D-operators.
The theorem states that, if P(D) is a polynomial D-operator, then, for any sufficiently differentiable function y,
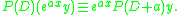
To prove the result, proceed by induction
. Note that only the special case
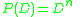
needs to be proved, since the general result then follows by linearity
of D-operators.
The result is clearly true for n = 1 since
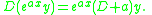
Now suppose the result true for n = k, that is,
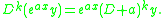
Then,
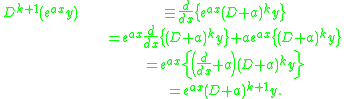
This completes the proof.
The shift theorem applied equally well to inverse operators:
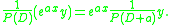
There is a similar version of the shift theorem for Laplace transforms ( ):
):
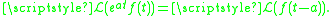
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the (exponential) shift theorem is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
differential operators (D-operators) and exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s. It permits one to eliminate, in certain cases, the exponential from under the D-operators.
The theorem states that, if P(D) is a polynomial D-operator, then, for any sufficiently differentiable function y,
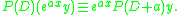
To prove the result, proceed by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. Note that only the special case
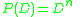
needs to be proved, since the general result then follows by linearity
Linearity of differentiation
In mathematics, the linearity of differentiation is a most fundamental property of the derivative, in differential calculus. It follows from the sum rule in differentiation and the constant factor rule in differentiation...
of D-operators.
The result is clearly true for n = 1 since
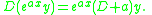
Now suppose the result true for n = k, that is,
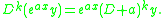
Then,
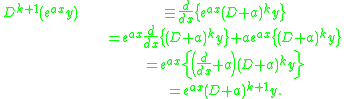
This completes the proof.
The shift theorem applied equally well to inverse operators:
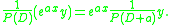
There is a similar version of the shift theorem for Laplace transforms (
 ):
):