
Shifting nth-root algorithm
Encyclopedia
The shifting nth root algorithm is an algorithm
for extracting the nth root
of a positive real number
which proceeds iteratively by shifting in n digits
of the radicand, starting with the most significant, and produces one digit of the root on each iteration, in a manner similar to long division
.
of the number system you are using, and n be the degree of the root to be extracted. Let x be the radicand processed thus far, y be the root extracted thus far, and r be the remainder. Let α be the next n digits of the radicand, and β be the next digit of the root. Let x' be the new value of x for the next iteration, y' be the new value of y for the next iteration, and r' be the new value of r for the next iteration. These are all integer
s.
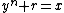 will hold. The invariant
will hold. The invariant 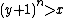 will hold. Thus y is the largest integer less than the nth root of x, and r is the remainder
will hold. Thus y is the largest integer less than the nth root of x, and r is the remainder
.
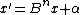 and we produce 1 digit of the root, so we have
and we produce 1 digit of the root, so we have 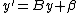 . We want to choose β and r
. We want to choose β and r' so that the invariants described above hold. It turns out that there is always exactly one such choice, as will be proved below.
The first invariant says that:

or
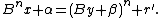
So, pick the largest integer β such that
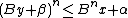
and let
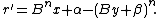
Such a β always exists, since if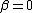 then the condition is
then the condition is 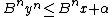 , but
, but 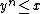 , so this is always true. Also, β must be less than B, since if
, so this is always true. Also, β must be less than B, since if 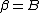 then we would have
then we would have
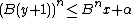
but the second invariant implies that
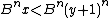
and since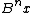 and
and  are both multiples of
are both multiples of  the difference between them must be at least
the difference between them must be at least 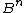 , and then we have
, and then we have
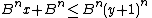
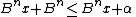
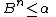
but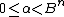 by definition of α, so this can't be true, and
by definition of α, so this can't be true, and 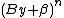 is a monotonically increasing function of β, so it can't be true for larger β either, so we conclude that there exists an integer γ with
is a monotonically increasing function of β, so it can't be true for larger β either, so we conclude that there exists an integer γ with  such that an integer r
such that an integer r' with 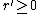 exists such that the first invariant holds if and only if
exists such that the first invariant holds if and only if 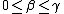 .
.
Now consider the second invariant. It says:
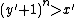
or

Now, if β is not the largest admissible β for the first invariant as described above, then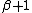 is also admissible, and we have
is also admissible, and we have
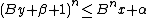
This violates the second invariant, so to satisfy both invariants we must pick the largest β allowed by the first invariant. Thus we have proven the existence and uniqueness of β and r' .
To summarize, on each iteration:
Now, note that , so the condition
, so the condition
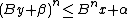
is equivalent to

and
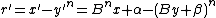
is equivalent to
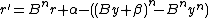
Thus, we don't actually need , and since
, and since 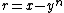 and
and 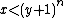 ,
, 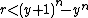 or
or  , or
, or  , so by using
, so by using  instead of
instead of  we save time and space by a factor of 1/n. Also, the
we save time and space by a factor of 1/n. Also, the  we subtract in the new test cancels the one in
we subtract in the new test cancels the one in  , so now the highest power of y we have to evaluate is
, so now the highest power of y we have to evaluate is 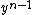 rather than
rather than 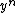 .
.
1. 4 4 2 2 4
----------------------
_ 3/ 3.000 000 000 000 000
\/ 1 = 300×(02)×1+30×0×(12)+13
-
2 000
1 744 = 300×(12)×4+30×1×(42)+43
-----
256 000
241 984 = 300×(142)×4+30×14×(42)+43
-------
14 016 000
12 458 888 = 300×(1442)×2+30×144×(22)+23
----------
1 557 112 000
1 247 791 448 = 300×(14422)×2+30×1442×(22)+23
-------------
309 320 552 000
249 599 823 424 = 300×(144222)×4+30×14422×(42)+43
---------------
59 720 728 576
Note that after the first iteration or two the leading term dominates the
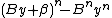 , so we can get an often correct first guess at β by dividing
, so we can get an often correct first guess at β by dividing 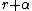 by
by 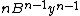 .
.
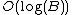 comparisons. Each comparison will require evaluating
comparisons. Each comparison will require evaluating 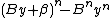 . In the kth iteration, y has k digits, and the polynomial can be evaluated with
. In the kth iteration, y has k digits, and the polynomial can be evaluated with 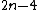 multiplications of up to
multiplications of up to 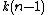 digits and
digits and  additions of up to
additions of up to 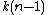 digits, once we know the powers of y and β up through
digits, once we know the powers of y and β up through  for y and n for β. β has a restricted range, so we can get the powers of β in constant time. We can get the powers of y with
for y and n for β. β has a restricted range, so we can get the powers of β in constant time. We can get the powers of y with  multiplications of up to
multiplications of up to 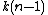 digits. Assuming n-digit multiplication takes time
digits. Assuming n-digit multiplication takes time 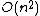 and addition takes time
and addition takes time 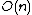 , we take time
, we take time
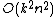 for each comparison, or time
for each comparison, or time 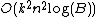 to pick β. The remainder of the algorithm is addition and subtraction that takes time
to pick β. The remainder of the algorithm is addition and subtraction that takes time 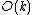 , so each iteration takes
, so each iteration takes 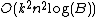 . For all k digits, we need time
. For all k digits, we need time 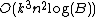 .
.
The only internal storage needed is r, which is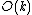 digits on the kth iteration. That this algorithm doesn't have bounded memory usage puts an upper bound on the number of digits which can be computed mentally, unlike the more elementary algorithms of arithmetic. Unfortunately, any bounded memory state machine with periodic inputs can only produce periodic outputs, so there are no such algorithms which can compute irrational numbers from rational ones, and thus no bounded memory root extraction algorithms.
digits on the kth iteration. That this algorithm doesn't have bounded memory usage puts an upper bound on the number of digits which can be computed mentally, unlike the more elementary algorithms of arithmetic. Unfortunately, any bounded memory state machine with periodic inputs can only produce periodic outputs, so there are no such algorithms which can compute irrational numbers from rational ones, and thus no bounded memory root extraction algorithms.
Note that increasing the base increases the time needed to pick β by a factor of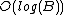 , but decreases the number of digits needed to achieve a given precision by the same factor, and since the algorithm is cubic time in the number of digits, increasing the base gives an overall speedup of
, but decreases the number of digits needed to achieve a given precision by the same factor, and since the algorithm is cubic time in the number of digits, increasing the base gives an overall speedup of 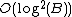 . When the base is larger than the radicand, the algorithm degenerates to binary search, so it follows that this algorithm is not useful for computing roots with a computer, as it is always outperformed by much simpler binary search, and has the same memory complexity.
. When the base is larger than the radicand, the algorithm degenerates to binary search, so it follows that this algorithm is not useful for computing roots with a computer, as it is always outperformed by much simpler binary search, and has the same memory complexity.
------------------
_ / 10.00 00 00 00 00 1
\/ 1 + 1
----- ----
1 00 100
0 + 0
-------- -----
1 00 00 1001
10 01 + 1
----------- ------
1 11 00 10101
1 01 01 + 1
---------- -------
1 11 00 101100
0 + 0
---------- --------
1 11 00 00 1011001
1 01 10 01 1
----------
1 01 11 remainder
----------------------
_ / 3.00 00 00 00 00
\/ 1 = 20×0×1+1^2
-
2 00
1 89 = 20×1×7+7^2
----
11 00
10 29 = 20×17×3+3^2
-----
71 00
69 24 = 20×173×2+2^2
-----
1 76 00
0 = 20×1732×0+0^2
-------
1 76 00 00
1 73 20 25 = 20×17320×5+5^2
----------
2 79 75
----------------------
_ 3/ 5.000 000 000 000 000
\/ 1 = 300×(0^2)×1+30×0×(1^2)+1^3
-
4 000
3 913 = 300×(1^2)×7+30×1×(7^2)+7^3
-----
87 000
0 = 300×(17^2)*0+30×17×(0^2)+0^3
-------
87 000 000
78 443 829 = 300×(170^2)×9+30×170×(9^2)+9^3
----------
8 556 171 000
7 889 992 299 = 300×(1709^2)×9+30×1709×(9^2)+9^3
-------------
666 178 701 000
614 014 317 973 = 300×(17099^2)×7+30×17099×(7^2)+7^3
---------------
52 164 383 027
---------------------------
_ 4/ 7.0000 0000 0000 0000 0000
\/ 1 = 4000×(0^3)×1+400×(0^2)×(1^2)+40×0×(1^3)+1^4
-
6 0000
5 5536 = 4000×(1^3)×6+600×(1^2)×(6^2)+40×1×(6^3)+6^4
------
4464 0000
3338 7536 = 4000×(16^3)×2+600*(16^2)×(2^2)+40×16×(2^3)+2^4
---------
1125 2464 0000
1026 0494 3376 = 4000×(162^3)×6+600×(162^2)×(6^2)+40×162×(6^3)+6^4
--------------
99 1969 6624 0000
86 0185 1379 0625 = 4000×(1626^3)×5+600×(1626^2)×(5^2)+
----------------- 40×1626×(5^3)+5^4
13 1784 5244 9375 0000
12 0489 2414 6927 3201 = 4000×(16265^3)×7+600×(16265^2)×(7^2)+
---------------------- 40×16265×(7^3)+7^4
1 1295 2830 2447 6799
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for extracting the nth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
of a positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
which proceeds iteratively by shifting in n digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
of the radicand, starting with the most significant, and produces one digit of the root on each iteration, in a manner similar to long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
.
Notation
Let B be the baseRadix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
of the number system you are using, and n be the degree of the root to be extracted. Let x be the radicand processed thus far, y be the root extracted thus far, and r be the remainder. Let α be the next n digits of the radicand, and β be the next digit of the root. Let x
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
Invariants
At each iteration, the invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
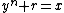 will hold. The invariant
will hold. The invariant 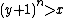 will hold. Thus y is the largest integer less than the nth root of x, and r is the remainder
will hold. Thus y is the largest integer less than the nth root of x, and r is the remainderRemainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
.
Initialization
The initial values of x, y, and r should be 0. The value of α for the first iteration should be the most significant aligned block of n digits of the radicand. An aligned block of n digits means a block of digits aligned so that the decimal point falls between blocks. For example, in 123.4 the most significant aligned block of 2 digits is 01, the next most significant is 23, and the third most significant is 40.Main loop
On each iteration we shift in n digits of the radicand, so we have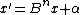 and we produce 1 digit of the root, so we have
and we produce 1 digit of the root, so we have 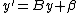 . We want to choose β and r
. We want to choose β and rThe first invariant says that:

or
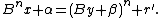
So, pick the largest integer β such that
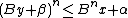
and let
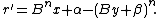
Such a β always exists, since if
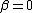 then the condition is
then the condition is 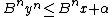 , but
, but 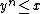 , so this is always true. Also, β must be less than B, since if
, so this is always true. Also, β must be less than B, since if 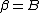 then we would have
then we would have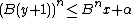
but the second invariant implies that
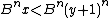
and since
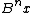 and
and  are both multiples of
are both multiples of  the difference between them must be at least
the difference between them must be at least 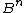 , and then we have
, and then we have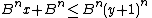
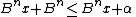
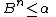
but
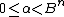 by definition of α, so this can't be true, and
by definition of α, so this can't be true, and 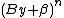 is a monotonically increasing function of β, so it can't be true for larger β either, so we conclude that there exists an integer γ with
is a monotonically increasing function of β, so it can't be true for larger β either, so we conclude that there exists an integer γ with  such that an integer r
such that an integer r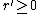 exists such that the first invariant holds if and only if
exists such that the first invariant holds if and only if 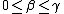 .
.Now consider the second invariant. It says:
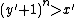
or

Now, if β is not the largest admissible β for the first invariant as described above, then
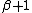 is also admissible, and we have
is also admissible, and we have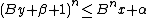
This violates the second invariant, so to satisfy both invariants we must pick the largest β allowed by the first invariant. Thus we have proven the existence and uniqueness of β and r
To summarize, on each iteration:
- Let α be the next aligned block of digits from the radicand
- Let
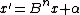
- Let β be the largest β such that

- Let
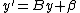
- Let
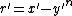
Now, note that
 , so the condition
, so the condition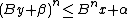
is equivalent to

and
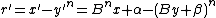
is equivalent to
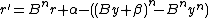
Thus, we don't actually need
 , and since
, and since 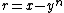 and
and 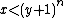 ,
, 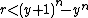 or
or  , or
, or  , so by using
, so by using  instead of
instead of  we save time and space by a factor of 1/n. Also, the
we save time and space by a factor of 1/n. Also, the  we subtract in the new test cancels the one in
we subtract in the new test cancels the one in  , so now the highest power of y we have to evaluate is
, so now the highest power of y we have to evaluate is 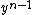 rather than
rather than 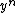 .
.Summary
- Initialize r and y to 0.
- Repeat until desired precision is obtained:
- Let α be the next aligned block of digits from the radicand.
- Let β be the largest β such that
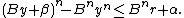
- Let
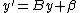 .
. - Let
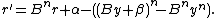
- Assign
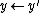 and
and 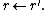
-
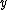 is the largest integer such that
is the largest integer such that 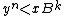 , and
, and 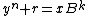 , where
, where 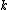 is the number of digits of the radicand after the decimal point that have been consumed (a negative number if the algorithm hasn't reached the decimal point yet).
is the number of digits of the radicand after the decimal point that have been consumed (a negative number if the algorithm hasn't reached the decimal point yet).
Paper-and-pencil nth roots
As noted above, this algorithm is similar to long division, and it lends itself to the same notation:1. 4 4 2 2 4
----------------------
_ 3/ 3.000 000 000 000 000
\/ 1 = 300×(02)×1+30×0×(12)+13
-
2 000
1 744 = 300×(12)×4+30×1×(42)+43
-----
256 000
241 984 = 300×(142)×4+30×14×(42)+43
-------
14 016 000
12 458 888 = 300×(1442)×2+30×144×(22)+23
----------
1 557 112 000
1 247 791 448 = 300×(14422)×2+30×1442×(22)+23
-------------
309 320 552 000
249 599 823 424 = 300×(144222)×4+30×14422×(42)+43
---------------
59 720 728 576
Note that after the first iteration or two the leading term dominates the
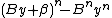 , so we can get an often correct first guess at β by dividing
, so we can get an often correct first guess at β by dividing 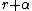 by
by 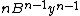 .
.Performance
On each iteration, the most time-consuming task is to select β. We know that there are B possible values, so we can find β using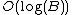 comparisons. Each comparison will require evaluating
comparisons. Each comparison will require evaluating 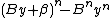 . In the kth iteration, y has k digits, and the polynomial can be evaluated with
. In the kth iteration, y has k digits, and the polynomial can be evaluated with 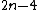 multiplications of up to
multiplications of up to 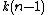 digits and
digits and  additions of up to
additions of up to 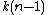 digits, once we know the powers of y and β up through
digits, once we know the powers of y and β up through  for y and n for β. β has a restricted range, so we can get the powers of β in constant time. We can get the powers of y with
for y and n for β. β has a restricted range, so we can get the powers of β in constant time. We can get the powers of y with  multiplications of up to
multiplications of up to 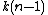 digits. Assuming n-digit multiplication takes time
digits. Assuming n-digit multiplication takes time 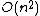 and addition takes time
and addition takes time 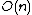 , we take time
, we take time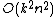 for each comparison, or time
for each comparison, or time 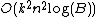 to pick β. The remainder of the algorithm is addition and subtraction that takes time
to pick β. The remainder of the algorithm is addition and subtraction that takes time 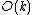 , so each iteration takes
, so each iteration takes 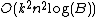 . For all k digits, we need time
. For all k digits, we need time 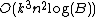 .
.The only internal storage needed is r, which is
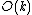 digits on the kth iteration. That this algorithm doesn't have bounded memory usage puts an upper bound on the number of digits which can be computed mentally, unlike the more elementary algorithms of arithmetic. Unfortunately, any bounded memory state machine with periodic inputs can only produce periodic outputs, so there are no such algorithms which can compute irrational numbers from rational ones, and thus no bounded memory root extraction algorithms.
digits on the kth iteration. That this algorithm doesn't have bounded memory usage puts an upper bound on the number of digits which can be computed mentally, unlike the more elementary algorithms of arithmetic. Unfortunately, any bounded memory state machine with periodic inputs can only produce periodic outputs, so there are no such algorithms which can compute irrational numbers from rational ones, and thus no bounded memory root extraction algorithms.Note that increasing the base increases the time needed to pick β by a factor of
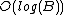 , but decreases the number of digits needed to achieve a given precision by the same factor, and since the algorithm is cubic time in the number of digits, increasing the base gives an overall speedup of
, but decreases the number of digits needed to achieve a given precision by the same factor, and since the algorithm is cubic time in the number of digits, increasing the base gives an overall speedup of 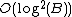 . When the base is larger than the radicand, the algorithm degenerates to binary search, so it follows that this algorithm is not useful for computing roots with a computer, as it is always outperformed by much simpler binary search, and has the same memory complexity.
. When the base is larger than the radicand, the algorithm degenerates to binary search, so it follows that this algorithm is not useful for computing roots with a computer, as it is always outperformed by much simpler binary search, and has the same memory complexity.Square root of 2 in binary
1. 0 1 1 0 1------------------
_ / 10.00 00 00 00 00 1
\/ 1 + 1
----- ----
1 00 100
0 + 0
-------- -----
1 00 00 1001
10 01 + 1
----------- ------
1 11 00 10101
1 01 01 + 1
---------- -------
1 11 00 101100
0 + 0
---------- --------
1 11 00 00 1011001
1 01 10 01 1
----------
1 01 11 remainder
Square root of 3
1. 7 3 2 0 5----------------------
_ / 3.00 00 00 00 00
\/ 1 = 20×0×1+1^2
-
2 00
1 89 = 20×1×7+7^2
----
11 00
10 29 = 20×17×3+3^2
-----
71 00
69 24 = 20×173×2+2^2
-----
1 76 00
0 = 20×1732×0+0^2
-------
1 76 00 00
1 73 20 25 = 20×17320×5+5^2
----------
2 79 75
Cube root of 5
1. 7 0 9 9 7----------------------
_ 3/ 5.000 000 000 000 000
\/ 1 = 300×(0^2)×1+30×0×(1^2)+1^3
-
4 000
3 913 = 300×(1^2)×7+30×1×(7^2)+7^3
-----
87 000
0 = 300×(17^2)*0+30×17×(0^2)+0^3
-------
87 000 000
78 443 829 = 300×(170^2)×9+30×170×(9^2)+9^3
----------
8 556 171 000
7 889 992 299 = 300×(1709^2)×9+30×1709×(9^2)+9^3
-------------
666 178 701 000
614 014 317 973 = 300×(17099^2)×7+30×17099×(7^2)+7^3
---------------
52 164 383 027
Fourth root of 7
1. 6 2 6 5 7---------------------------
_ 4/ 7.0000 0000 0000 0000 0000
\/ 1 = 4000×(0^3)×1+400×(0^2)×(1^2)+40×0×(1^3)+1^4
-
6 0000
5 5536 = 4000×(1^3)×6+600×(1^2)×(6^2)+40×1×(6^3)+6^4
------
4464 0000
3338 7536 = 4000×(16^3)×2+600*(16^2)×(2^2)+40×16×(2^3)+2^4
---------
1125 2464 0000
1026 0494 3376 = 4000×(162^3)×6+600×(162^2)×(6^2)+40×162×(6^3)+6^4
--------------
99 1969 6624 0000
86 0185 1379 0625 = 4000×(1626^3)×5+600×(1626^2)×(5^2)+
----------------- 40×1626×(5^3)+5^4
13 1784 5244 9375 0000
12 0489 2414 6927 3201 = 4000×(16265^3)×7+600×(16265^2)×(7^2)+
---------------------- 40×16265×(7^3)+7^4
1 1295 2830 2447 6799
External links
- Why the square root algorithm works "Home School Math". Also related pages giving examples of the long-division-like pencil and paper method for square roots.

