
Signal averaging
Encyclopedia
Signal averaging is a signal processing
technique applied in the time domain
, intended to increase the strength of a signal relative to noise
that is obscuring it. By averaging a set of replicate
measurements, the signal-to-noise ratio
, S/N, will be increased, ideally in proportion to the square root of the number of measurements.
Under these assumptions let the signal strength be denoted by S and let the standard deviation
of a single measurement be σ; this represents the noise in one measurement, N. If n measurements are added together the sum of signal strengths will be nS. For the noise, the standard error propagation formula shows that the variance
, σ2, is additive. The variance of the sum is equal to nσ2. Hence the signal-to-noise ratio, S/N, is given by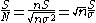
The equivalent expression for signal averaging is obtained by dividing both numerator and denominator by n.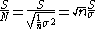
Thus, in the ideal case S/N increases with the square root of the number of measurements that are averaged. In practice, the assumptions may be not be fully realized. This will result in a lower S/N improvement than in the ideal case, but in many cases near-ideal S/N improvement can be achieved..
% create [sz x sz] matrix
% fill the matrix with noise
sz=256;
NOISE_TRIALS=randn(sz);
% create signal with a sine wave
% divide the array SZ by sz/2
SZ=1:sz;
SZ=SZ/(sz/2);
S=sin(2*pi*SZ);
for i=1:sz;
NOISE_TRIALS(i,:) = NOISE_TRIALS(i,:) + S;
end;
% create the average
average=sum(NOISE_TRIALS)/sz;
odd_average=sum(NOISE_TRIALS(1:2:sz,:))/(sz/2);
even_average=sum(NOISE_TRIALS(2:2:sz,:))/(sz/2);
noise_estimate=odd_average-even_average;
% create plot
figure
hold
plot(NOISE_TRIALS(1,:),'g')
plot(noise_estimate,'k')
plot(average,'r')
plot(S)
xlabel('Trials')
ylabel('Amplitude')
title('Signal Averaging')
gtext('Signal: Blue')
gtext('Single trial: Green')
gtext('Noise estimate: Black')
gtext('Average: Red')
The averaging process above, and in general, results in an estimate of the signal. When compared with the raw trace, the averaged noise component is reduced with every averaged trial. When averaging real signals, the underlying component may not always be as clear, resulting in repeated averages in a search for consistent components in two or three replicates. It is unlikely that two or more consistent results will be produced by chance alone.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
technique applied in the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
, intended to increase the strength of a signal relative to noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
that is obscuring it. By averaging a set of replicate
Replication (statistics)
In engineering, science, and statistics, replication is the repetition of an experimental condition so that the variability associated with the phenomenon can be estimated. ASTM, in standard E1847, defines replication as "the repetition of the set of all the treatment combinations to be compared in...
measurements, the signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
, S/N, will be increased, ideally in proportion to the square root of the number of measurements.
The ideal case
Ideally it is assumed that- Signal and noise are uncorrelated.
- Signal strength is constant in the replicate measurements.
- Noise is random, with a meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of zero and constant varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
in the replicate measurements.
Under these assumptions let the signal strength be denoted by S and let the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of a single measurement be σ; this represents the noise in one measurement, N. If n measurements are added together the sum of signal strengths will be nS. For the noise, the standard error propagation formula shows that the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, σ2, is additive. The variance of the sum is equal to nσ2. Hence the signal-to-noise ratio, S/N, is given by
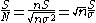
The equivalent expression for signal averaging is obtained by dividing both numerator and denominator by n.
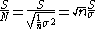
Thus, in the ideal case S/N increases with the square root of the number of measurements that are averaged. In practice, the assumptions may be not be fully realized. This will result in a lower S/N improvement than in the ideal case, but in many cases near-ideal S/N improvement can be achieved..
Time-Locked Signals
Averaging is applied to enhance a time-locked signal component in noisy measurements.Averaging Odd and Even Trials
A specific way of obtaining replicates is to average all the odd and even trials in separate buffers. This has the advantage of allowing for comparison of even and odd results from interleaved trials. An average of odd and even averages generates the completed averaged result, while the difference between the odd and even averages constitutes an estimate of the noise.Algorithmic Implementation
The following is a MATLAB simulation of the averaging process:% create [sz x sz] matrix
% fill the matrix with noise
sz=256;
NOISE_TRIALS=randn(sz);
% create signal with a sine wave
% divide the array SZ by sz/2
SZ=1:sz;
SZ=SZ/(sz/2);
S=sin(2*pi*SZ);
for i=1:sz;
NOISE_TRIALS(i,:) = NOISE_TRIALS(i,:) + S;
end;
% create the average
average=sum(NOISE_TRIALS)/sz;
odd_average=sum(NOISE_TRIALS(1:2:sz,:))/(sz/2);
even_average=sum(NOISE_TRIALS(2:2:sz,:))/(sz/2);
noise_estimate=odd_average-even_average;
% create plot
figure
hold
plot(NOISE_TRIALS(1,:),'g')
plot(noise_estimate,'k')
plot(average,'r')
plot(S)
xlabel('Trials')
ylabel('Amplitude')
title('Signal Averaging')
gtext('Signal: Blue')
gtext('Single trial: Green')
gtext('Noise estimate: Black')
gtext('Average: Red')
The averaging process above, and in general, results in an estimate of the signal. When compared with the raw trace, the averaged noise component is reduced with every averaged trial. When averaging real signals, the underlying component may not always be as clear, resulting in repeated averages in a search for consistent components in two or three replicates. It is unlikely that two or more consistent results will be produced by chance alone.
Non-random Noise
Signal averaging typically relies heavily on the assumption that the noise component of a signal is random, having zero mean, and being unrelated to the signal. However, there are instances in which the noise is not random. A common example of non-random noise is a hum (e.g. 60 Hz noise originating from power lines). To apply the signal averaging technique, a few critical adaptations must be made, and the problem can be avoided by:- Randomizing the stimulus interval, or
- Using a noninteger stimulus rate (e.g. 3.4 Hz instead of 3.0 Hz)

