
Signed-digit representation
Encyclopedia
Signed-digit representation of numbers indicates that digits can be prefixed with a − (minus) sign to indicate that they are negative.
Signed-digit representation can be used in low-level software and hardware to accomplish fast addition of integers because it can eliminate carries. In the binary numeral system
one special case of signed-digit representation is the non-adjacent form
which can offer speed benefits with minimal space overhead.
 to
to 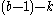 , where typically
, where typically 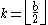 . For balanced forms, odd base numbers are advantageous. With an odd base number, truncation and rounding become the same operation, and all the digits except 0 are used in both positive and negative form.
. For balanced forms, odd base numbers are advantageous. With an odd base number, truncation and rounding become the same operation, and all the digits except 0 are used in both positive and negative form.
A notable example is balanced ternary
, where the base is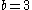 , and the numerals have the values −1, 0 and +1 (rather than 0, 1, and 2 as in the standard ternary numeral system
, and the numerals have the values −1, 0 and +1 (rather than 0, 1, and 2 as in the standard ternary numeral system
). Balanced ternary uses the minimum number of digits in a balanced form. Balanced decimal uses digits from −5 to +4. Balanced base nine, with digits from −4 to +4 provides the advantages of an odd-base balanced form with a similar number of digits, and is easy to convert to and from balanced ternary.
Other notable examples include Booth encoding and non-adjacent form
, both of which use a base of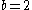 , and both of which use numerals with the values −1, 0, and +1 (rather than 0 and 1 as in the standard binary numeral system
, and both of which use numerals with the values −1, 0, and +1 (rather than 0 and 1 as in the standard binary numeral system
).
The non-adjacent form does guarantee a unique representation for every integer value, as do balanced forms.
When representations are extended to fractional numbers, uniqueness is lost for non-adjacent and balanced forms; for example,
and
Such examples can be shown to exist by considering the greatest and smallest possible representations with integral parts 0 and 1 respectively, and then noting that they are equal. (Indeed, this works with any integral-base system.)
Signed-digit representation can be used in low-level software and hardware to accomplish fast addition of integers because it can eliminate carries. In the binary numeral system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
one special case of signed-digit representation is the non-adjacent form
Non-adjacent form
The non-adjacent form of a number is a unique signed-digit representation. Like the name suggests, non-zero values cannot be adjacent. For example:2 = 4 + 2 + 1 = 72 = 8 − 2 + 1 = 72 = 8 − 4 + 2 + 1 = 72 = 8 − 1 = 7...
which can offer speed benefits with minimal space overhead.
Balanced form
In balanced form, the digits are drawn from a range to
to 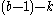 , where typically
, where typically 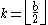 . For balanced forms, odd base numbers are advantageous. With an odd base number, truncation and rounding become the same operation, and all the digits except 0 are used in both positive and negative form.
. For balanced forms, odd base numbers are advantageous. With an odd base number, truncation and rounding become the same operation, and all the digits except 0 are used in both positive and negative form.A notable example is balanced ternary
Balanced ternary
Balanced ternary is a non-standard positional numeral system , useful for comparison logic. It is a ternary system, but unlike the standard ternary system, the digits have the values −1, 0, and 1...
, where the base is
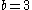 , and the numerals have the values −1, 0 and +1 (rather than 0, 1, and 2 as in the standard ternary numeral system
, and the numerals have the values −1, 0 and +1 (rather than 0, 1, and 2 as in the standard ternary numeral systemTernary numeral system
Ternary is the base- numeral system. Analogous to a bit, a ternary digit is a trit . One trit contains \log_2 3 bits of information...
). Balanced ternary uses the minimum number of digits in a balanced form. Balanced decimal uses digits from −5 to +4. Balanced base nine, with digits from −4 to +4 provides the advantages of an odd-base balanced form with a similar number of digits, and is easy to convert to and from balanced ternary.
Other notable examples include Booth encoding and non-adjacent form
Non-adjacent form
The non-adjacent form of a number is a unique signed-digit representation. Like the name suggests, non-zero values cannot be adjacent. For example:2 = 4 + 2 + 1 = 72 = 8 − 2 + 1 = 72 = 8 − 4 + 2 + 1 = 72 = 8 − 1 = 7...
, both of which use a base of
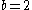 , and both of which use numerals with the values −1, 0, and +1 (rather than 0 and 1 as in the standard binary numeral system
, and both of which use numerals with the values −1, 0, and +1 (rather than 0 and 1 as in the standard binary numeral systemBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
).
Non-unique representations
Note that signed-digit representation is not necessarily unique. For instance:- (0 1 1 1)2 = 4 + 2 + 1 = 7
- (1 0 −1 1)2 = 8 − 2 + 1 = 7
- (1 −1 1 1)2 = 8 − 4 + 2 + 1 = 7
- (1 0 0 −1)2 = 8 − 1 = 7
The non-adjacent form does guarantee a unique representation for every integer value, as do balanced forms.
When representations are extended to fractional numbers, uniqueness is lost for non-adjacent and balanced forms; for example,
- (0 . (1 0) …)NAF = = (1 . (0 −1) …)NAF
and
- (0 . 4 4 4 …)(10bal) = = (1 . -5 -5 -5 …)(10bal)
Such examples can be shown to exist by considering the greatest and smallest possible representations with integral parts 0 and 1 respectively, and then noting that they are equal. (Indeed, this works with any integral-base system.)

