Similarity solution
Encyclopedia
In fluid dynamics
, a similarity solution is a form of solution in which at least one co-ordinate lacks a distinguished origin; more physically, it describes a flow which 'looks the same' either at all times, or at all length scales. These include, for example, the Blasius boundary layer
or the Sedov-Taylor shell
.
and scaling laws; by looking at the physical effects present in a system we may estimate their size and hence which, for example, might be neglected. If we have catalogued these effects we will occasionally find that the system has not fixed a natural lengthscale (timescale), but that the solution depends on space (time). It is then necessary to construct a lengthscale (timescale) using time (space) and the other dimensional quantities present - such as the viscosity
. These constructs are not 'guessed' but are derived immediately from the scaling of the governing equations.
the wall is made to move with constant speed 
in a fixed direction (for definiteness, say the 
direction and consider only the 
plane). We can see that there is no distinguished length scale given in the problem, and we have the boundary conditions of no slip
on 
and that the plate have no effect on the fluid at infinity
as 
.
Now, if we examine the Navier-Stokes equations
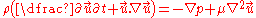
we can observe that this flow will be rectilinear
, with gradients in the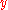
direction and flow in the 
direction, and that the pressure term will have no tangential component so that
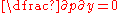. The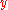 
component of the Navier-Stokes equations then becomes
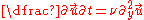
and we may apply scaling arguments to show that
which gives us the scaling of the
co-ordinate as
.
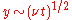This allows us to pose an self-similar ansatz such that, with
and 
dimensionless,
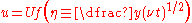
We have now extracted all of the relevant physics and need only solve the equations; for many cases this will need to be done numerically. This equation is
with solution satisfying the boundary conditions that
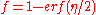or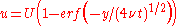 
which is a self-similar solution of the first kind.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, a similarity solution is a form of solution in which at least one co-ordinate lacks a distinguished origin; more physically, it describes a flow which 'looks the same' either at all times, or at all length scales. These include, for example, the Blasius boundary layer
Blasius boundary layer
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow U....
or the Sedov-Taylor shell
Blast wave
A blast wave in fluid dynamics is the pressure and flow resulting from the deposition of a large amount of energy in a small very localised volume. The flow field can be approximated as a lead shock wave, followed by a 'self-similar' subsonic flow field. In simpler terms, a blast wave is an area of...
.
Concept
A powerful tool in physics is the concept of dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
and scaling laws; by looking at the physical effects present in a system we may estimate their size and hence which, for example, might be neglected. If we have catalogued these effects we will occasionally find that the system has not fixed a natural lengthscale (timescale), but that the solution depends on space (time). It is then necessary to construct a lengthscale (timescale) using time (space) and the other dimensional quantities present - such as the viscosity
. These constructs are not 'guessed' but are derived immediately from the scaling of the governing equations.Example - The impulsively started plate
Consider a semi-infinite domain bounded by a rigid wall and filled with viscous fluid. At time the wall is made to move with constant speed in a fixed direction (for definiteness, say the direction and consider only the plane). We can see that there is no distinguished length scale given in the problem, and we have the boundary conditions of no slip on and that the plate have no effect on the fluid at infinity
as .Now, if we examine the Navier-Stokes equations
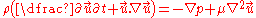
we can observe that this flow will be rectilinear
Rectilinear
Rectilinear may refer to:* Rectilinear grid, a tessellation of the Euclidean plane* Rectilinear lens, a photographic lens* Rectilinear locomotion, a form of animal locomotion* Rectilinear polygon, a polygon whose edges meet at right angles...
, with gradients in the
direction and flow in the direction, and that the pressure term will have no tangential component so that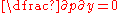. The 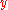component of the Navier-Stokes equations then becomes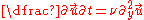and we may apply scaling arguments to show that
which gives us the scaling of the
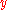co-ordinate as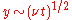.This allows us to pose an self-similar ansatz such that, with
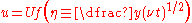
and dimensionless,We have now extracted all of the relevant physics and need only solve the equations; for many cases this will need to be done numerically. This equation is
with solution satisfying the boundary conditions that
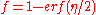or 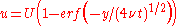which is a self-similar solution of the first kind.