Simple rational approximation
Encyclopedia
Simple rational approximation (SRA) is a subset of interpolating methods using rational functions. Especially, SRA interpolates a given function with a specific rational function
whose poles
and zeros are simple
, which means that there is no multiplicity in poles and zeros. Sometimes, it only implies simple poles.
The main application of SRA lies in finding the zeros of secular functions. A divide-and-conquer algorithm to find the eigenvalues and eigenvectors for various kinds of matrices
is well-known in numerical analysis
. In a strict sense, SRA implies a specific interpolation
using simple rational functions as a part of the divide-and-conquer algorithm. Since such secular functions consist of a series of rational functions with simple poles, SRA is the best candidate to interpolate the zeros of the secular function. Moreover, based on previous researches, a simple zero that lies between two adjacent poles can be considerably well interpolated by using a two-dominant-pole rational function as an approximating function.
. Halley's formula is known as one-point third-order iterative method to solve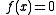
by means of approximating a rational function defined by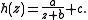
We can determine a, b, and c so that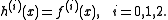
Then solving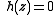
yields the iteration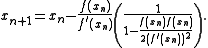
This is referred to as Halley's formula.
This geometrical interpretation
was derived by Gander(1978), where the equivalent iteration also was derived by applying Newton's method to
We call this algebraic interpretation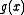
of Halley's formula.
There are no known explanation for how one is supposed to calculate a, b or c out of these equations.
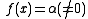using simple rational approximation by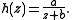
Then we need to evaluate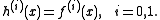
Thus we have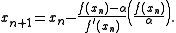
The algebraic interpretation of this iteration is obtained by solving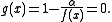
This one-point second-order method is known to show a locally quadratic convergence if the root of equation is simple.
SRA strictly implies this one-point second-order interpolation by a simple rational function.
We can notice that even third order method is a variation of Newton's method. We see the Newton's steps are multiplied by some factors. These factors are called the convergence factors of the variations, which are useful for analyzing the rate of convergence. See Gander(1978).
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
whose poles
Poles
thumb|right|180px|The state flag of [[Poland]] as used by Polish government and diplomatic authoritiesThe Polish people, or Poles , are a nation indigenous to Poland. They are united by the Polish language, which belongs to the historical Lechitic subgroup of West Slavic languages of Central Europe...
and zeros are simple
Simple
Simple may refer to:- Technology :*SIMPLE, an instant messaging protocol*SiMPLE, a programming development system*SIMPLE algorithm, a widely used numerical procedure...
, which means that there is no multiplicity in poles and zeros. Sometimes, it only implies simple poles.
The main application of SRA lies in finding the zeros of secular functions. A divide-and-conquer algorithm to find the eigenvalues and eigenvectors for various kinds of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is well-known in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
. In a strict sense, SRA implies a specific interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
using simple rational functions as a part of the divide-and-conquer algorithm. Since such secular functions consist of a series of rational functions with simple poles, SRA is the best candidate to interpolate the zeros of the secular function. Moreover, based on previous researches, a simple zero that lies between two adjacent poles can be considerably well interpolated by using a two-dominant-pole rational function as an approximating function.
One-point third-order iterative method: Halley's formula
The origin of the interpolation with rational functions can be found in the previous work done by Edmond HalleyEdmond Halley
Edmond Halley FRS was an English astronomer, geophysicist, mathematician, meteorologist, and physicist who is best known for computing the orbit of the eponymous Halley's Comet. He was the second Astronomer Royal in Britain, following in the footsteps of John Flamsteed.-Biography and career:Halley...
. Halley's formula is known as one-point third-order iterative method to solve
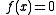by means of approximating a rational function defined by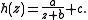We can determine a, b, and c so that
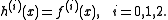
Then solving
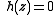yields the iteration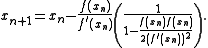This is referred to as Halley's formula.
This geometrical interpretation
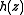was derived by Gander(1978), where the equivalent iteration also was derived by applying Newton's method to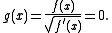We call this algebraic interpretation
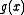of Halley's formula.There are no known explanation for how one is supposed to calculate a, b or c out of these equations.
One-point second-order iterative method: Simple rational approximation
Similarly, we can derive a variation of Halley's formula based on a one-point second-order iterative method to solve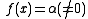 using simple rational approximation by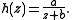Then we need to evaluate
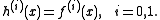
Thus we have
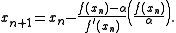
The algebraic interpretation of this iteration is obtained by solving
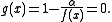
This one-point second-order method is known to show a locally quadratic convergence if the root of equation is simple.
SRA strictly implies this one-point second-order interpolation by a simple rational function.
We can notice that even third order method is a variation of Newton's method. We see the Newton's steps are multiplied by some factors. These factors are called the convergence factors of the variations, which are useful for analyzing the rate of convergence. See Gander(1978).