Simplicial category
Encyclopedia
In mathematics, the simplex category (or simplicial category or ordinal category) is the category
of finite ordinals and order preserving maps. It is used to define simplicial
and cosimplicial objects.
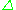and is sometimes denoted by Ord. There are several equivalent descriptions of this category. 
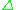can be described as the category of finite ordinals as objects, thought of as totally ordered sets, and order preserving functions as morphisms. The category is generated by coface and codegeneracy maps, which amount to inserting or deleting elements of the orderings. (See simplicial set
for relations of these maps.)
A simplicial object is a presheaf on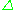
, that is a contravariant functor from 
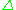to another category. For instance, simplicial set
s are contravariant with codomain category the category of sets. A cosimplicial object is defined similarly as a covariant functor originating from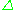
. Note that in topology a simplicial object defined in this way would be called an augmented simplicial object because of the presence of an augmentation map. This map can be dropped to yield a traditionally defined simplicial object.
An algebraic definition identifies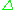
as the freely generated monoidal category
on a single monoidal generator. This description is useful for understanding how any comonoid object in a monoidal category gives rise to a simplicial object since it can then be viewed as the image of a functor from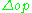
to the monoidal category containing the comonoid. Similarly, this also illuminates the construction of simplicial sets from monads (and hence adjoint functors
) since monads can be viewed as monoid objects in endofunctors categories
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of finite ordinals and order preserving maps. It is used to define simplicial
Simplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
and cosimplicial objects.
Formal definition
The simplex category is usually denoted by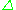 and is sometimes denoted by Ord. There are several equivalent descriptions of this category. 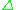can be described as the category of finite ordinals as objects, thought of as totally ordered sets, and order preserving functions as morphisms. The category is generated by coface and codegeneracy maps, which amount to inserting or deleting elements of the orderings. (See simplicial setSimplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
for relations of these maps.)
A simplicial object is a presheaf on
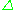, that is a contravariant functor from 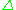to another category. For instance, simplicial setSimplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s are contravariant with codomain category the category of sets. A cosimplicial object is defined similarly as a covariant functor originating from
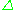. Note that in topology a simplicial object defined in this way would be called an augmented simplicial object because of the presence of an augmentation map. This map can be dropped to yield a traditionally defined simplicial object.An algebraic definition identifies
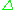as the freely generated monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
on a single monoidal generator. This description is useful for understanding how any comonoid object in a monoidal category gives rise to a simplicial object since it can then be viewed as the image of a functor from
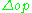to the monoidal category containing the comonoid. Similarly, this also illuminates the construction of simplicial sets from monads (and hence adjoint functorsAdjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
) since monads can be viewed as monoid objects in endofunctors categories
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
.