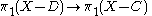Simply connected at infinity
Encyclopedia
In topology
, a branch of mathematics, a topological space
X is said to be simply connected at infinity if for all compact
subsets C of X, there is a compact set D in X containing C so that the induced map
is trivial. Intuitively, this is the property that loops far away from a small subspace of X can be collapsed, no matter how bad the small subspace is.
The Whitehead manifold
is an example of a 3-manifold
that is contractible but not simply connected at infinity. Since this property is invariant under homeomorphism
, this proves that the Whitehead manifold is not homeomorphic to R3. However, it is a theorem that any contractible n-manifold which is also simply connected at infinity is homeomorphic to Rn.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a branch of mathematics, a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is said to be simply connected at infinity if for all compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subsets C of X, there is a compact set D in X containing C so that the induced map
is trivial. Intuitively, this is the property that loops far away from a small subspace of X can be collapsed, no matter how bad the small subspace is.
The Whitehead manifold
Whitehead manifold
In mathematics, the Whitehead manifold is an open 3-manifold that is contractible, but not homeomorphic to R3. Henry Whitehead discovered this puzzling object while he was trying to prove the Poincaré conjecture....
is an example of a 3-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
that is contractible but not simply connected at infinity. Since this property is invariant under homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
, this proves that the Whitehead manifold is not homeomorphic to R3. However, it is a theorem that any contractible n-manifold which is also simply connected at infinity is homeomorphic to Rn.