
Simpson's rule
Encyclopedia
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Simpson's rule is a method for numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
, the numerical approximation of definite integrals. Specifically, it is the following approximation:

Simpson's rule also corresponds to the 3-point Newton-Cotes quadrature rule
Newton-Cotes formulas
In numerical analysis, the Newton–Cotes formulae, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulae for numerical integration based on evaluating the integrand at equally-spaced points...
.
The method is credited to the mathematician Thomas Simpson
Thomas Simpson
Thomas Simpson FRS was a British mathematician, inventor and eponym of Simpson's rule to approximate definite integrals...
(1710–1761) of Leicestershire, England. Kepler used similar formulas over 100 years prior and in German the method is sometimes called Keplersche Fassregel for this reason.
Simpson's rule is a staple of scientific data analysis and engineering. It is widely used, for example, by Naval architects
Naval architecture
Naval architecture is an engineering discipline dealing with the design, construction, maintenance and operation of marine vessels and structures. Naval architecture involves basic and applied research, design, development, design evaluation and calculations during all stages of the life of a...
to calculate the capacity of a ship or lifeboat
Lifeboat (shipboard)
A lifeboat is a small, rigid or inflatable watercraft carried for emergency evacuation in the event of a disaster aboard ship. In the military, a lifeboat may be referred to as a whaleboat, dinghy, or gig. The ship's tenders of cruise ships often double as lifeboats. Recreational sailors sometimes...
.
Quadratic interpolation
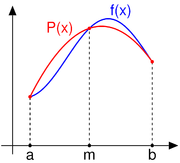
One derivation replaces the integrand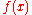 by the quadratic polynomial
by the quadratic polynomialQuadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
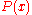 which takes the same values as
which takes the same values as 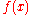 at the end points a and b and the midpoint m = (a + b) / 2. One can use Lagrange polynomial interpolation
at the end points a and b and the midpoint m = (a + b) / 2. One can use Lagrange polynomial interpolationLagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
to find an expression for this polynomial,
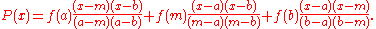
An easy (albeit tedious) calculation shows that

This calculation can be carried out more easily if one first observes that (by scaling) there is no loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
in assuming that
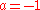 and
and  .
.Averaging the midpoint and the trapezoidal rules
Another derivation constructs Simpson's rule from two simpler approximations: the midpoint rule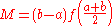
and the trapezoidal rule
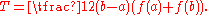
The errors in these approximations are

respectively. It follows that the leading error term vanishes if we take the weighted average
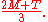
This weighted average is exactly Simpson's rule.
Using another approximation (for example, the trapezoidal rule with twice as many points), it is possible to take a suitable weighted average and eliminate another error term. This is Romberg's method
Romberg's method
In numerical analysis, Romberg's method is used to estimate the definite integral \int_a^b f \, dx by applying Richardson extrapolation repeatedly on the trapezium rule or the rectangle rule . The estimates generate a triangular array...
.
Undetermined coefficients
The third derivation starts from the ansatzAnsatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
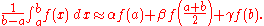
The coefficients α, β and γ can be fixed by requiring that this approximation be exact for all quadratic polynomials. This yields Simpson's rule.
Error
The error in approximating an integral by Simpson's rule is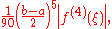
where
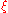 is some number between
is some number between  and
and  .
.The error is asymptotically proportional to
 . However, the above derivations suggest an error proportional to
. However, the above derivations suggest an error proportional to 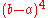 . Simpson's rule gains an extra order because the points at which the integrand is evaluated are distributed symmetrically in the interval [a, b].
. Simpson's rule gains an extra order because the points at which the integrand is evaluated are distributed symmetrically in the interval [a, b].Simpson's rule provides exact results for any polynomial of degree three or less, since the error term involves the fourth derivative of f.
Composite Simpson's rule
If the interval of integration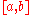 is in some sense "small", then Simpson's rule will provide an adequate approximation to the exact integral. By small, what we really mean is that the function being integrated is relatively smooth over the interval
is in some sense "small", then Simpson's rule will provide an adequate approximation to the exact integral. By small, what we really mean is that the function being integrated is relatively smooth over the interval 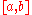 . For such a function, a smooth quadratic interpolant like the one used in Simpson's rule will give good results.
. For such a function, a smooth quadratic interpolant like the one used in Simpson's rule will give good results.However, it is often the case that the function we are trying to integrate is not smooth over the interval. Typically, this means that either the function is highly oscillatory, or it lacks derivatives at certain points. In these cases, Simpson's rule may give very poor results. One common way of handling this problem is by breaking up the interval
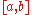 into a number of small subintervals. Simpson's rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson's rule.
into a number of small subintervals. Simpson's rule is then applied to each subinterval, with the results being summed to produce an approximation for the integral over the entire interval. This sort of approach is termed the composite Simpson's rule.Suppose that the interval
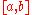 is split up in
is split up in  subintervals, with
subintervals, with  an even number. Then, the composite Simpson's rule is given by
an even number. Then, the composite Simpson's rule is given by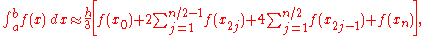
where
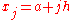 for
for  with
with  ; in particular,
; in particular,  and
and 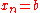 . The above formula can also be written as
. The above formula can also be written as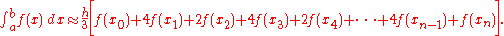
The error committed by the composite Simpson's rule is bounded (in absolute value) by

where
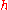 is the "step length", given by
is the "step length", given by 
This formulation splits the interval
 in subintervals of equal length. In practice, it is often advantageous to use subintervals of different lengths, and concentrate the efforts on the places where the integrand is less well-behaved. This leads to the adaptive Simpson's method
in subintervals of equal length. In practice, it is often advantageous to use subintervals of different lengths, and concentrate the efforts on the places where the integrand is less well-behaved. This leads to the adaptive Simpson's methodAdaptive Simpson's method
Adaptive Simpson's method, also called adaptive Simpson's rule, is a method of numerical integration proposed by G.F. Kuncir in 1962. It is probably the first recursive adaptive algorithm for numerical integration to appear in print, although more modern adaptive methods based on Gauss–Kronrod...
.
Alternative extended Simpson's rule
This is another formulation of a composite Simpson's rule: instead of applying Simpson's rule to disjoint segments of the integral to be approximated, Simpson's rule is applied to overlapping segments, yielding: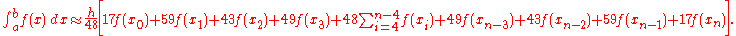
Simpson's 3/8 rule
Simpson's 3/8 rule is another method for numerical integration proposed by Thomas Simpson. It is based upon a cubic interpolation rather than a quadratic interpolation. Simpson's 3/8 rule is as follows: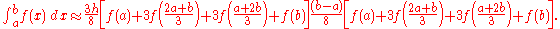
The error of this method is:
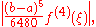
where
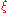 is some number between
is some number between  and
and  . Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value. A composite 3/8 rule also exists, similarly as above.
. Thus, the 3/8 rule is about twice as accurate as the standard method, but it uses one more function value. A composite 3/8 rule also exists, similarly as above.Simpson's 3/8 rule is used by Naval architects to calculate a merchant cargo ship's lifeboat capacity.
Sample implementation
An implementation of the composite Simpson's rule in pylab:def simpson(f, a, b, n):
"""f=function, a=initial value, b=end value, n=number of double intervals of size 2h"""
n *= 2
h = (b - a) / n;
S = f(a)
for i in range(1, n, 2):
x = a + h * i
S += 4 * f(x)
for i in range(2, n-1, 2):
x = a + h * i
S += 2 * f(x)
S += f(b)
F = h * S / 3
return F
External links
- Simpson's Rule for Numerical Integration
- Application of Simpson's Rule - Earthwork Excavation (Note: The formula described in this page is correct but there are errors in the calculation which should give a result of 569m3 and not 623m3 as stated)
- Simpson's 1/3rd rule of integration - Notes, PPT, Mathcad, Matlab, Mathematica, Maple at Numerical Methods for STEM undergraduate
- A detailed description of a computer implementation is described by Dorai Sitaram in Teach Yourself Scheme in Fixnum Days, Appendix C
- C Language Program to Implement Simpson's Rule

