Structural and reduced form

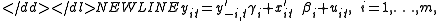
where i is the equation number, and is the observation index. In these equations x_it is the k_i×1 vector of exogenous variables, y_it is the dependent variable, y_−i,t is the n_i×1 vector of all other endogenous variables which enter the i^th equation on the right-hand side, and u_it are the error terms. The “−i” notation indicates that the vector y_−i,t may contain any of the y’s except for y_it (since it is already present on the left-hand side). The regression coefficients β_i and γ_i are of dimensions k_i×1 and n_i×1 correspondingly. Vertically stacking the T observations corresponding to the i^th equation, we can write each equation in vector form as

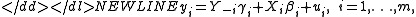
where y_i and u_i are T×1 vectors, X_i is a T×k_i matrix of exogenous regressors, and Y_−i is a T×n_i matrix of endogenous regressors on the right-hand side of the i^th equation. Finally, we can move all endogenous variables to the left-hand side and write the m equations jointly in vector form as

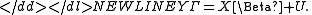
This representation is known as the structural form. In this equation is the T×m matrix of dependent variables. Each of the matrices Y_−i is in fact an n_i-columned submatrix of this Y. The m×m matrix Γ, which describes the relation between the dependent variables, has a complicated structure. It has ones on the diagonal, and all other elements of each column i are either the components of the vector −γ_i or zeros, depending on which columns of Y were included in the matrix Y_−i. The T×k matrix X contains all exogenous regressors from all equations, but without repetitions (that is, matrix X should be of full rank). Thus, each X_i is a k_i-columned submatrix of X. Matrix Β has size k×m, and each of its columns consists of the components of vectors β_i and zeros, depending on which of the regressors from X were included or excluded from X_i. Finally, is a T×m matrix of the error terms.

Postmultiplying the structural equation by , the system can be written in the reduced form as

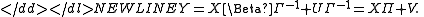
This is already a simple general linear model

General linear model

The general linear model is a statistical linear model.It may be written aswhere Y is a matrix with series of multivariate measurements, X is a matrix that might be a design matrix, B is a matrix containing parameters that are usually to be estimated and U is a matrix containing errors or...

, and it can be estimated for example by ordinary least squares

Ordinary least squares

In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...

. Unfortunately, the task of decomposing the estimated matrix $\backslash scriptstyle\backslash hat\backslash Pi$ into the individual factors Β and is quite complicated, and therefore the reduced form is more suitable for prediction but not inference.

Assumptions

Firstly, the rank of the matrix X of exogenous regressors must be equal to k, both in finite samples and in the limit as (this later requirement means that in the limit the expression $\backslash scriptstyle\; \backslash frac1TX\text{'}\backslash !X$ should converge to a nondegenerate k×k matrix). Matrix Γ is also assumed to be non-degenerate.

Secondly, error terms are assumed to be serially independent and identically distributed. That is, if the t^th row of matrix U is denoted by u_(t), then the sequence of vectors {u_(t)} should be iid, with zero mean and some covariance matrix Σ (which is unknown). In particular, this implies that , and .

Lastly, the identification conditions requires that the number of unknowns in this system of equations should not exceed the number of equations. More specifically, the order condition requires that for each equation , which can be phrased as “the number of excluded exogenous variables is greater or equal to the number of included endogenous variables”. The rank condition of identifiability is that , where Π_i0 is a matrix which is obtained from Π by crossing out those columns which correspond to the excluded endogenous variables, and those rows which correspond to the included exogenous variables.

Two-stages least squares (2SLS)

The simplest and the most common estimation method for the simultaneous equations model is the so-called two-stage least squares method, developed independently by and . It is an equation-by-equation technique, where the endogenous regressors on the right-hand side of each equation are being instrumented with the regressors X from all other equations. The method is called “two-stage” because it conducts estimation in two steps:

Step 1: Regress Y_−i on X and obtain the predicted values $\backslash scriptstyle\backslash hat\{Y\}\_\{\backslash !-i\}$;

Step 2: Estimate γ_i, β_i by the ordinary least squares

Ordinary least squares

In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...

 regression of y_i on $\backslash scriptstyle\backslash hat\{Y\}\_\{\backslash !-i\}$ and X_i.

If the i^th equation in the model is written as

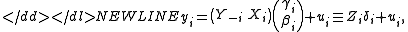
where Z_i is a T×(n_i + k_i) matrix of both endogenous and exogenous regressors in the i^th equation, and δ_i is an (n_i + k_i)-dimensional vector of regression coefficients, then the 2SLS estimator of δ_i will be given by

where is the projection matrix onto the linear space spanned by the exogenous regressors X.

Indirect least squares

Indirect least squares is an approach in econometrics

Econometrics

Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...

 where the coefficient

Coefficient

In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

s in a simultaneous equations model are estimated from the reduced form

Reduced form

In statistics, and particularly in econometrics, the reduced form of a system of equations is the result of solving the system for the endogenous variables. This gives the latter as a function of the exogenous variables, if any...

 model using ordinary least squares

Ordinary least squares

In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...

. For this, the structural system of equations is transformed into the reduced form first. Once the coefficients are estimated the model is put back into the structural form.

Limited information maximum likelihood (LIML)

The “limited information” maximum likelihood method was suggested by . The explicit formula for this estimator is:

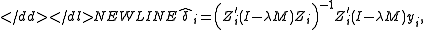
where , , and λ is the smallest characteristic root of the matrix

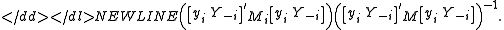
Note that when the LIML estimator coincides with the 2SLS estimator.

Three-stage least squares (3SLS)

The three-stage least squares estimator was introduced by . It combines two-stage least squares (2SLS) with seemingly unrelated regressions (SUR).

See also

• General linear model
  General linear model
  The general linear model is a statistical linear model.It may be written aswhere Y is a matrix with series of multivariate measurements, X is a matrix that might be a design matrix, B is a matrix containing parameters that are usually to be estimated and U is a matrix containing errors or...
  
  
• Seemingly unrelated regressions
• Indirect least squares

External links

• About.com:economics Online dictionary of economics, entry for ILS

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.