Simultaneous perturbation stochastic approximation
Encyclopedia
Simultaneous perturbation stochastic approximation (SPSA) is an algorithmic method for optimizing systems with multiple unknown parameters. It is a type of stochastic approximation
algorithm. As an optimization method, it is appropriately suited to large-scale population models, adaptive modeling, simulation optimization, and atmospheric model
ing. Many examples are presented at the SPSA website.
SPSA is a descent method capable of finding global minima.
Its main feature is the gradient approximation that requires
only two measurements of the objective function, regardless
of the dimension of the optimization problem. Recall
that we want to find the optimal control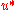
with loss
function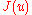
:
Both Finite Differences Stochastic Approximation (FDSA)
and SPSA use the same iterative process:
where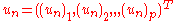
represents the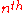
iterate,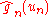
is the estimate of the gradient of the objective
function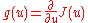
evaluated at 
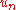, and 
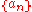is a positive number sequence converging to 0. If 
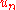is a p-dimension vector, the 
component of the symmetric finite difference
gradient estimator is:
FD: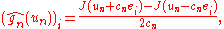
1 ≤i ≤p where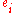
is the unit vector with a 1 in the 
place, and
is a small positive number that decreases with n. With this method, 2p evaluations of J for each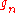 
are needed. Clearly, when p is large, this estimator loses efficiency.
SP: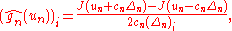
Remark that FD perturbs only one direction at a time, while
the SP estimator disturbs all directions at the same time (the
numerator is identical in all p components). The number of
loss function measurements needed in the SPSA method for
each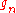
is always 2, independent of the dimension p. Thus, SPSA uses p times fewer function evaluations than FDSA, which makes it a lot more efficient.
Simple experiments with p=2 showed that SPSA converges
in the same number of iterations as FDSA. The latter
follows approximately the steepest descent direction, behaving
like the gradient method. On the other
hand, SPSA, with the random search direction, does not follow
exactly the gradient path. In average though, it tracks it
nearly because the gradient approximation is an almost unbiased
estimator of the gradient, as shown in the following
lemma
Lemma 1 Denote by
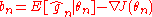
the bias in the estimator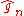
. Assume that 
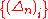are
all mutually independent with zero-mean, bounded second
moments, and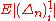
uniformly bounded on U. Then 
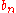→ w.p. 1.
The main idea is to use conditioning
on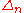
to express 
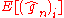and then to use a second
order Taylor expansion of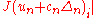
and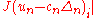 
.
After algebraic manipulations implying the zero mean and
the independence of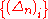
, we get
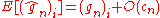
The result follows from the hypothesis that
→0..
Next we resume some of the hypotheses under which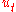
converges in probability to the set of global minima of 
.
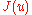The efficiency of
the method depends on the shape of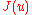
, the values of the parameters 
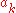and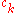 
and the distribution of the perturbation terms 
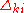. First, the algorithm parameters must satisfy the
following conditions:
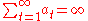; good choice would be 
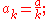, a>0;
A good choice for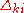
is Bernoulli +-1 with probability 0.5. The uniform and normal distributions do not satisfy the finite moment conditions, so can not be used.
The loss function J(u) must be thrice continuously differentiable and the individual elements of the third derivative must be bounded:
. Also, |J(u)|→∝ as u→∝.
In addition,
must be Lipschitz continuous, bounded and the ODE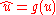 
must have a unique solution for each initial condition.
Under these conditions and a few others,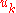
converges in probability to the set of global minima of J(u).
Stochastic approximation
Stochastic approximation methods are a family of iterative stochastic optimization algorithms that attempt to find zeroes or extrema of functions which cannot be computed directly, but only estimated via noisy observations....
algorithm. As an optimization method, it is appropriately suited to large-scale population models, adaptive modeling, simulation optimization, and atmospheric model
Atmospheric model
An atmospheric model is a mathematical model constructed around the full set of primitive dynamical equations which govern atmospheric motions. It can supplement these equations with parameterizations for turbulent diffusion, radiation, moist processes , heat exchange, soil, vegetation, surface...
ing. Many examples are presented at the SPSA website.
SPSA is a descent method capable of finding global minima.
Its main feature is the gradient approximation that requires
only two measurements of the objective function, regardless
of the dimension of the optimization problem. Recall
that we want to find the optimal control
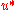with lossfunction
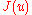:Both Finite Differences Stochastic Approximation (FDSA)
and SPSA use the same iterative process:
where
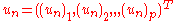
represents the
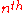
iterate,
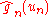is the estimate of the gradient of the objectivefunction
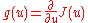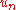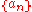evaluated at , and is a positive number sequence converging to 0. If 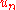is a p-dimension vector, the component of the symmetric finite difference
gradient estimator is:
FD:
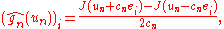
1 ≤i ≤p where
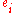is the unit vector with a 1 in the place, and
is a small positive number that decreases with n. With this method, 2p evaluations of J for each 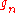are needed. Clearly, when p is large, this estimator loses efficiency.SP:
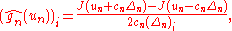
Remark that FD perturbs only one direction at a time, while
the SP estimator disturbs all directions at the same time (the
numerator is identical in all p components). The number of
loss function measurements needed in the SPSA method for
each
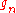is always 2, independent of the dimension p. Thus, SPSA uses p times fewer function evaluations than FDSA, which makes it a lot more efficient.Simple experiments with p=2 showed that SPSA converges
in the same number of iterations as FDSA. The latter
follows approximately the steepest descent direction, behaving
like the gradient method. On the other
hand, SPSA, with the random search direction, does not follow
exactly the gradient path. In average though, it tracks it
nearly because the gradient approximation is an almost unbiased
estimator of the gradient, as shown in the following
lemma
Lemma 1 Denote by
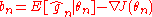
the bias in the estimator
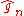. Assume that 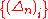areall mutually independent with zero-mean, bounded second
moments, and
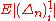uniformly bounded on U. Then 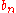→ w.p. 1.The main idea is to use conditioning
on
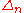to express 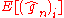and then to use a secondorder Taylor expansion of
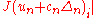and 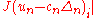.After algebraic manipulations implying the zero mean and
the independence of
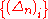, we get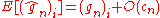The result follows from the hypothesis that
→0..Next we resume some of the hypotheses under which
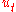converges in probability to the set of global minima of 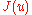.The efficiency of
the method depends on the shape of
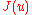, the values of the parameters 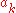and 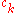and the distribution of the perturbation terms 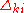. First, the algorithm parameters must satisfy thefollowing conditions:
-
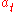>0,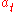 
→0 when t→∝ and
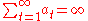; good choice would be 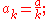, a>0;
-
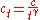, where c>0, 
; -
-
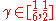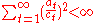
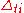must be mutually independent zero-mean random variables, symmetrically distributed about zero, with 
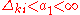and 
a.s., ∀i, k.
A good choice for
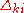is Bernoulli +-1 with probability 0.5. The uniform and normal distributions do not satisfy the finite moment conditions, so can not be used.The loss function J(u) must be thrice continuously differentiable and the individual elements of the third derivative must be bounded:
. Also, |J(u)|→∝ as u→∝.In addition,
must be Lipschitz continuous, bounded and the ODE 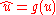must have a unique solution for each initial condition.Under these conditions and a few others,
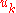converges in probability to the set of global minima of J(u).