Skewes' number
Encyclopedia
In number theory
, Skewes' number is any of several extremely large numbers used by the South Africa
n mathematician Stanley Skewes
as upper bound
s for the smallest natural number
x for which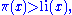
where π is the prime-counting function and li is the logarithmic integral function
. These bounds have since been improved by others: there is a crossing near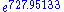
. It is not known whether it is the smallest.
, Skewes' teacher, proved (in ) that there is such a number (and so, a first such number); and indeed found that the sign of the difference π(x) − li(x) changes infinitely often. All numerical evidence then available seemed to suggest that π(x) is always less than li(x), though mathematicians familiar with Riemann's work on the Riemann zeta function would probably have realized that occasional exceptions were likely by the argument given below (and the claim sometimes made that Littlewood's result was a big surprise to experts seems doubtful). Littlewood's proof did not, however, exhibit a concrete such number x.
proved that, assuming that the Riemann hypothesis
is true, there exists a number x violating π(x) < li(x) below
In , without assuming the Riemann hypothesis, Skewes managed to prove that there must exist a value of x below
Skewes' task was to make Littlewood's existence proof effective: exhibiting some concrete upper bound for the first sign change. According to George Kreisel, this was at the time not considered obvious even in principle. The approach called unwinding
in proof theory
looks directly at proofs and their structure to produce bounds. The other way, more often seen in practice in number theory, changes proof structure enough so that absolute constants can be made more explicit.
Although both Skewes' numbers are big compared to most numbers encountered in mathematical proofs, neither is anywhere near as big as Graham's number
.
showed that somewhere between 1.53 and 1.65 there are more than 10500 consecutive integers x with π(x) > li(x).
Without assuming the Riemann hypothesis, proved an upper bound of 7. A better estimation was 1.39822 discovered by , who showed there are at least 10153 consecutive integers somewhere near this value where π(x) > li(x), and suggested that there are probably at least 10311. gave a small improvement and correction to the result of Bays and Hudson. Bays and Hudson found a few much smaller values of x where π(x) gets close to li(x); the possibility that there are crossover points near these values does not seem to have been definitely ruled out yet, though computer calculations suggest they are unlikely to exist. find a smaller interval for a crossing, which was slightly improved by .
Rigorously, proved that there are no crossover points below x = 108, and this lower bound was subsequently improved by to 8, and by to 1014.
There is no explicit value x known for certain to have the property π(x) > li(x), though computer calculations suggest some explicit numbers that are quite likely to satisfy this.
showed that the proportion of integers for which π(x)>li(x) is positive, and showed that this proportion is about .00000026, which is surprisingly large given how far one has to go to find the first example.
where the sum is over zeros ρ of the Riemann zeta function. The largest error term in the approximation π(x) = li(x) (if the Riemann hypothesis
is true) is li/2, showing that li(x) is usually larger than π(x). The other terms above are somewhat smaller, and moreover tend to have different complex arguments so mostly cancel out. Occasionally however, many of the larger ones might happen to have roughly the same complex argument, in which case they will reinforce each other instead of cancelling and will overwhelm the term li/2. The reason why the Skewes number is so large is that these smaller terms are quite a lot smaller than the leading error term, mainly because the first complex zero of the zeta function has quite a large imaginary part, so a large number (several hundred) of them need to have roughly the same argument in order to overwhelm the dominant term. The chance of N random complex numbers having roughly the same argument is about 1 in 2N. This explains why π(x) is sometimes larger than li(x), and also why it is rare for this to happen. It also shows why finding places where this happens depends on large scale calculations of millions of high precision zeros of the Riemann zeta function. The argument above is not a proof, as it assumes the zeros of the Riemann zeta function are random which is not true. Roughly speaking, Littlewood's proof consists of Dirichlet's approximation theorem
to show that sometimes many terms have about the same argument.
In the event that the Riemann hypothesis is false, the argument is much simpler, essentially because the terms li(xρ) for zeros violating the Riemann hypothesis (with real part greater than 1/2) are eventually larger than li(x1/2).
The reason for the term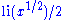
is that, roughly speaking, 
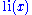counts not primes, but powers of primes 
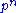weighted by 
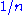, and 
is a sort of correction term coming from squares of primes.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Skewes' number is any of several extremely large numbers used by the South Africa
South Africa
The Republic of South Africa is a country in southern Africa. Located at the southern tip of Africa, it is divided into nine provinces, with of coastline on the Atlantic and Indian oceans...
n mathematician Stanley Skewes
Stanley Skewes
Stanley Skewes was a South African mathematician, best known for his discovery of Skewes number in 1933. He was one of John Edensor Littlewood's students at Cambridge University.-Publications:...
as upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
s for the smallest natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
x for which
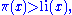
where π is the prime-counting function and li is the logarithmic integral function
Logarithmic integral function
In mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...
. These bounds have since been improved by others: there is a crossing near
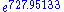. It is not known whether it is the smallest.Skewes' numbers
John Edensor LittlewoodJohn Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
, Skewes' teacher, proved (in ) that there is such a number (and so, a first such number); and indeed found that the sign of the difference π(x) − li(x) changes infinitely often. All numerical evidence then available seemed to suggest that π(x) is always less than li(x), though mathematicians familiar with Riemann's work on the Riemann zeta function would probably have realized that occasional exceptions were likely by the argument given below (and the claim sometimes made that Littlewood's result was a big surprise to experts seems doubtful). Littlewood's proof did not, however, exhibit a concrete such number x.
proved that, assuming that the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is true, there exists a number x violating π(x) < li(x) below
In , without assuming the Riemann hypothesis, Skewes managed to prove that there must exist a value of x below
Skewes' task was to make Littlewood's existence proof effective: exhibiting some concrete upper bound for the first sign change. According to George Kreisel, this was at the time not considered obvious even in principle. The approach called unwinding
Proof mining
In proof theory, a branch of mathematical logic, proof mining is a research program that analyzes formalized proofs, especially in analysis, to obtain explicit bounds or rates of convergence from proofs that, when expressed in natural language, appear to be nonconstructive.This research has led to...
in proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
looks directly at proofs and their structure to produce bounds. The other way, more often seen in practice in number theory, changes proof structure enough so that absolute constants can be made more explicit.
Although both Skewes' numbers are big compared to most numbers encountered in mathematical proofs, neither is anywhere near as big as Graham's number
Graham's number
Graham's number, named after Ronald Graham, is a large number that is an upper bound on the solution to a certain problem in Ramsey theory.The number gained a degree of popular attention when Martin Gardner described it in the "Mathematical Games" section of Scientific American in November 1977,...
.
More recent estimates
These (enormous) upper bounds have since been reduced considerably by using large scale computer calculations of zeros of the Riemann zeta function. The first estimate for the actual value of a crossover point was given by , whoshowed that somewhere between 1.53 and 1.65 there are more than 10500 consecutive integers x with π(x) > li(x).
Without assuming the Riemann hypothesis, proved an upper bound of 7. A better estimation was 1.39822 discovered by , who showed there are at least 10153 consecutive integers somewhere near this value where π(x) > li(x), and suggested that there are probably at least 10311. gave a small improvement and correction to the result of Bays and Hudson. Bays and Hudson found a few much smaller values of x where π(x) gets close to li(x); the possibility that there are crossover points near these values does not seem to have been definitely ruled out yet, though computer calculations suggest they are unlikely to exist. find a smaller interval for a crossing, which was slightly improved by .
Rigorously, proved that there are no crossover points below x = 108, and this lower bound was subsequently improved by to 8, and by to 1014.
There is no explicit value x known for certain to have the property π(x) > li(x), though computer calculations suggest some explicit numbers that are quite likely to satisfy this.
showed that the proportion of integers for which π(x)>li(x) is positive, and showed that this proportion is about .00000026, which is surprisingly large given how far one has to go to find the first example.
Riemann's formula
Riemann gave an explicit formula for π(x), whose leading terms are (ignoring some subtle convergence questions)where the sum is over zeros ρ of the Riemann zeta function. The largest error term in the approximation π(x) = li(x) (if the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
is true) is li/2, showing that li(x) is usually larger than π(x). The other terms above are somewhat smaller, and moreover tend to have different complex arguments so mostly cancel out. Occasionally however, many of the larger ones might happen to have roughly the same complex argument, in which case they will reinforce each other instead of cancelling and will overwhelm the term li/2. The reason why the Skewes number is so large is that these smaller terms are quite a lot smaller than the leading error term, mainly because the first complex zero of the zeta function has quite a large imaginary part, so a large number (several hundred) of them need to have roughly the same argument in order to overwhelm the dominant term. The chance of N random complex numbers having roughly the same argument is about 1 in 2N. This explains why π(x) is sometimes larger than li(x), and also why it is rare for this to happen. It also shows why finding places where this happens depends on large scale calculations of millions of high precision zeros of the Riemann zeta function. The argument above is not a proof, as it assumes the zeros of the Riemann zeta function are random which is not true. Roughly speaking, Littlewood's proof consists of Dirichlet's approximation theorem
Dirichlet's approximation theorem
In number theory, Dirichlet's theorem on Diophantine approximation, also called Dirichlet's approximation theorem, states that for any real number α and any positive integer N, there exists integers p and q such that 1 ≤ q ≤ N and...
to show that sometimes many terms have about the same argument.
In the event that the Riemann hypothesis is false, the argument is much simpler, essentially because the terms li(xρ) for zeros violating the Riemann hypothesis (with real part greater than 1/2) are eventually larger than li(x1/2).
The reason for the term
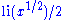is that, roughly speaking, 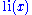counts not primes, but powers of primes 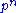weighted by 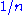, and is a sort of correction term coming from squares of primes.External links
- Patrick Demichel. The prime counting function and related subjects. http://web.archive.org/web/20060908033007/http://demichel.net/patrick/li_crossover_pi.pdf retrieved 2009-09-29