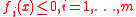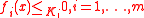Slater's condition
Encyclopedia
In mathematics
, Slater's condition (or Slater condition) is a sufficient condition for strong duality to hold for a convex optimization problem. This is a specific example of a constraint qualification. In particular, if Slater's condition holds for the primal problem, then the duality gap
is 0, and if the dual value is finite then it is attained.
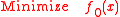
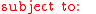
with
convex
(and therefore a convex optimization problem). Then strong duality holds if there exists an
(where relint is the relative interior
and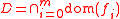
) such that
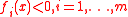and
If the first
constraints, 
are linear function
s, then strong duality holds if there exists an
such that
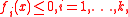
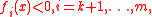and
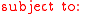
where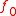
is convex and 
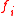is 
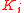-convex for each 
. Then Slater's condition says that if there exists an 
such that
and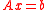
then strong duality holds.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Slater's condition (or Slater condition) is a sufficient condition for strong duality to hold for a convex optimization problem. This is a specific example of a constraint qualification. In particular, if Slater's condition holds for the primal problem, then the duality gap
Duality gap
In optimization problems in applied mathematics, the duality gap is the difference between the primal and dual solutions. If d^* is the optimal dual value and p^* is the optimal primal value then the duality gap is equal to p^* - d^*. This value is always greater than or equal to 0. The duality...
is 0, and if the dual value is finite then it is attained.
Mathematics
Given the problem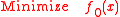
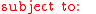
with
convexConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
(and therefore a convex optimization problem). Then strong duality holds if there exists an
(where relint is the relative interiorRelative interior
In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces...
and
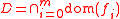) such that 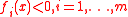andIf the first
constraints, are linear functionLinear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
s, then strong duality holds if there exists an
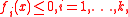
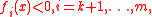such that andGeneralized Inequalities
Given the problem
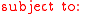
where
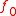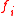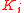is convex and is -convex for each . Then Slater's condition says that if there exists an such that and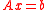then strong duality holds.