
Slope field
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
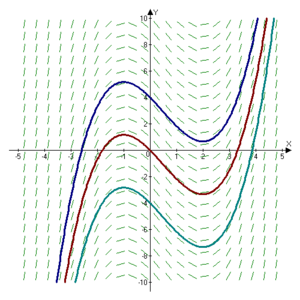
, a slope field (or direction field) is a graphical representation of the solutions of a first-order differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
. It is achieved without solving the differential equation analytically, and thus it is useful. The representation may be used to qualitatively visualize solutions, or to numerically approximate them.
Standard case
The slope field is traditionally defined for the following type of differential equations .
.It can be viewed as a creative way to plot a real-valued function of two real variables
 as a planar picture. Specifically, for a given pair
as a planar picture. Specifically, for a given pair  , a vector with the components
, a vector with the components  is drawn at the point
is drawn at the point  on the
on the  -plane. Sometimes, the vector
-plane. Sometimes, the vector  is normalized to make the plot better looking for a human eye. A set of pairs
is normalized to make the plot better looking for a human eye. A set of pairs  making a rectangular grid is typically used for the drawing.
making a rectangular grid is typically used for the drawing.An Isocline
Isocline
thumb|right|300px|Fig. 1: Isoclines , slope field , and some solution curves of y'=xyAn Isocline is a curve through points at which the parent function's slope will always be the same, regardless of initial conditions...
(a series of lines with the same slope) is often used to supplement the slope field. In an equation of the form
 , the isocline is a line in the
, the isocline is a line in the  -plane plane obtained by setting
-plane plane obtained by setting  equal to a constant.
equal to a constant.General case of a system of differential equations
Given a system of differential equations,

the slope field is an array of slope marks in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
(in any number of dimensions depending on the number of relevant variables; for example, two in the case of a first-order linear ODE
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
, as seen to the right). Each slope mark is centered at a point
 and is parallel to the vector
and is parallel to the vector .
.The number, position, and length of the slope marks can be arbitrary. The positions are usually chosen such that the points
 make a uniform grid. The standard case, described above, represents
make a uniform grid. The standard case, described above, represents  . The general case of the slope field for systems of differential equations is not easy to visualize for
. The general case of the slope field for systems of differential equations is not easy to visualize for  .
.General application
With computers, complicated slope fields can be quickly made without tedium, and so only recently practical application is to use them merely to get the feel for what a solution should be before an explicit general solution is sought. Of course, computers can also just solve for one, if it exists.If there is no explicit general solution, computers can use slope fields (even if they aren’t shown) to numerically find graphical solutions. Examples of such routines are Euler's method, or better, the Runge-Kutta methods.
Example code in GNU OctaveGNU OctaveGNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
/MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
Ffun = @(X,Y)X.*Y; % function f(x,y)=xy
[X,Y]=meshgrid(-2:.3:2,-2:.3:2); % choose the plot sizes
DY=Ffun(X,Y); DX=ones(size(DY)); % generate the plot values
quiver(X,Y,DX,DY); % plot the direction field
hold on;
contour(X,Y,DY,[-6 -2 -1 0 1 2 6]); %add the isoclines
title('Slope field and isoclines for f(x,y)=xy')
See also
- Examples of differential equationsExamples of differential equationsDifferential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists....
- Differential equations of mathematical physics
- Differential equations from outside physics
- Laplace transform applied to differential equations
- List of dynamical systems and differential equations topics



