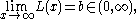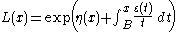Slowly varying function
Encyclopedia
In real analysis
, a branch of mathematics
, a slowly varying function is a function resembling a function converging at infinity. A regularly varying function resembles a power law
function near infinity. Slowly varying and regularly varying functions are important in probability theory
.

If the limit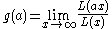
is finite but nonzero for every a > 0, the function L is called a regularly varying function.
These definitions are due to Jovan Karamata
.
Regular variation is the subject of
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a slowly varying function is a function resembling a function converging at infinity. A regularly varying function resembles a power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
function near infinity. Slowly varying and regularly varying functions are important in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
Definition
A function L: (0,∞) → (0, ∞) is called slowly varying (at infinity) if for all a > 0,
If the limit
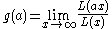
is finite but nonzero for every a > 0, the function L is called a regularly varying function.
These definitions are due to Jovan Karamata
Jovan Karamata
Jovan Karamata was one of the greatest Serbian mathematicians of the 20th century. He is remembered for contributions to analysis, in particular, the Tauberian theory and the theory of slowly varying functions...
.
Regular variation is the subject of
Examples
- If L has a limit
-
- then L is a slowly varying function.
- For any β∈R, the function L(x)= logβ x is slowly varying.
- The function L(x)=x is not slowly varying, neither is L(x)=xβ for any real β;≠0. However, they are regularly varying.
Properties
Some important properties are :- The limit in the definition is uniform if a is restricted to a finite interval.
- Karamata's characterization theorem: every regularly varying function is of the form x βL(x) where β ≥ 0 and L is a slowly varying function. That is, the function g(a) in the definition has to be of the form λρ; the number ρ is called the index of regular variation.
- Representation theorem: a function L is slowly varying if and only if there exists B > 0 such that for all x ≥ B the function can be written in the form
- where η(x) converges to a finite number and ε(x) converges to zero as x goes to infinity, and both functions are measurable and bounded.