
Socialist millionaire
Encyclopedia
The Socialist Millionaire Problem is one in which two millionaires want to determine if their wealth is equal, without disclosing any information about their riches to each other. It is a variant of the Millionaire's Problem whereby two millionaires wish to compare their riches to determine who has the most wealth, without disclosing any information about their riches to each other.
It is often used as a cryptographic protocol
that allows two parties to verify the identity of the remote party through the use of a shared secret, avoiding a man-in-the-middle attack without the inconvenience of manually comparing public key fingerprints through an outside channel. In effect a relatively weak password/passphrase in natural language can be used.
 , and
, and 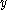 respectively. Alice and Bob wish to learn if
respectively. Alice and Bob wish to learn if 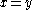 without allowing either party to learn anything else about the other's secret value. A passive attacker, simply spying on the messages Alice and Bob exchange learns nothing about
without allowing either party to learn anything else about the other's secret value. A passive attacker, simply spying on the messages Alice and Bob exchange learns nothing about  and
and 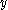 , nor even if
, nor even if  . Even if one of the parties is dishonest, and deviates from the protocol, he or she cannot learn anything more than if
. Even if one of the parties is dishonest, and deviates from the protocol, he or she cannot learn anything more than if  . An active attacker, capable of arbitrarily interfering with Alice and Bob's communication (a man-in-the-middle
. An active attacker, capable of arbitrarily interfering with Alice and Bob's communication (a man-in-the-middle
) cannot learn more than a passive attacker, and cannot affect the outcome of the protocol other than to make it fail. Therefore, the protocol can be used to authenticate whether two parties have the same secret information. Popular instant message cryptography package Off-the-Record Messaging
uses the Socialist Millionaire protocol for authentication, in which the secrets and
and 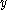 contain information about both parties' long-term authentication public keys, as well as information entered by the users themselves.
contain information about both parties' long-term authentication public keys, as well as information entered by the users themselves.
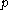 , or in other words, in the multiplicative group
, or in other words, in the multiplicative group
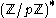 . Let
. Let 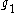 be a generator
be a generator
of the group (any element other than 1, noting that 0 is not an element of multiplicative groups). The values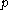 and
and 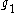 are agreed on before the protocol, and in practice are generally fixed in a given implementation. For example, in Off-the-Record Messaging
are agreed on before the protocol, and in practice are generally fixed in a given implementation. For example, in Off-the-Record Messaging 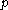 is a specific fixed 1536-bit prime. All sent values include zero-knowledge proofs that they were generated according to this protocol, as indicated in the detailed description below.
is a specific fixed 1536-bit prime. All sent values include zero-knowledge proofs that they were generated according to this protocol, as indicated in the detailed description below.
Assuming that Alice begins the exchange:
The correctness of this algorithm (but not its security) can be shown by simply representing all values in terms of the inputs ,
, 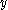 , and
, and 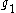 , and the randomly generated values
, and the randomly generated values 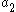 ,
, 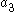 ,
, 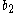 ,
, 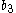 ,
,  , and
, and  :
:
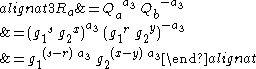
Assuming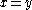 , then
, then 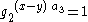 , and therefore
, and therefore 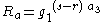 . The same logic holds to show
. The same logic holds to show  . Therefore,
. Therefore,
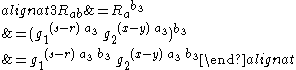
Similarly expanding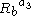 reveals that the values of
reveals that the values of 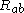 that Alice and Bob generate are identical. Finally, examining the equation being tested by Alice and Bob shows that the algorithm works:
that Alice and Bob generate are identical. Finally, examining the equation being tested by Alice and Bob shows that the algorithm works:
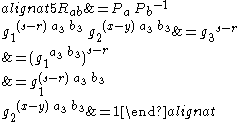
As the last equation given above holds only if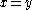 , and as it is equivalent to the first equation, the tests Alice and Bob perform of
, and as it is equivalent to the first equation, the tests Alice and Bob perform of 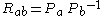 are therefore equivalent to testing
are therefore equivalent to testing 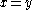 , completing a proof of correctness.
, completing a proof of correctness.
However, as written above the protocol is vulnerable to poisoning whereby either Alice or Bob chooses (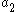 ,
, 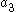 ) or (
) or (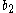 ,
, 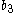 ) to be zero to be able to predict the result http://weizenspr.eu/2009/der-strippende-sozialistische-millionar/. To solve this problem, check that the pairs (
) to be zero to be able to predict the result http://weizenspr.eu/2009/der-strippende-sozialistische-millionar/. To solve this problem, check that the pairs (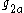 ,
, 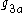 ) and (
) and (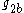 ,
, 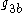 ) are not equal to one.
) are not equal to one.
It is often used as a cryptographic protocol
Cryptographic protocol
A security protocol is an abstract or concrete protocol that performs a security-related function and applies cryptographic methods.A protocol describes how the algorithms should be used...
that allows two parties to verify the identity of the remote party through the use of a shared secret, avoiding a man-in-the-middle attack without the inconvenience of manually comparing public key fingerprints through an outside channel. In effect a relatively weak password/passphrase in natural language can be used.
Motivation
Alice and Bob have secret values , and
, and 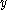 respectively. Alice and Bob wish to learn if
respectively. Alice and Bob wish to learn if 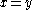 without allowing either party to learn anything else about the other's secret value. A passive attacker, simply spying on the messages Alice and Bob exchange learns nothing about
without allowing either party to learn anything else about the other's secret value. A passive attacker, simply spying on the messages Alice and Bob exchange learns nothing about  and
and 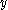 , nor even if
, nor even if  . Even if one of the parties is dishonest, and deviates from the protocol, he or she cannot learn anything more than if
. Even if one of the parties is dishonest, and deviates from the protocol, he or she cannot learn anything more than if  . An active attacker, capable of arbitrarily interfering with Alice and Bob's communication (a man-in-the-middle
. An active attacker, capable of arbitrarily interfering with Alice and Bob's communication (a man-in-the-middleMan-in-the-middle attack
In cryptography, the man-in-the-middle attack , bucket-brigade attack, or sometimes Janus attack, is a form of active eavesdropping in which the attacker makes independent connections with the victims and relays messages between them, making them believe that they are talking directly to each other...
) cannot learn more than a passive attacker, and cannot affect the outcome of the protocol other than to make it fail. Therefore, the protocol can be used to authenticate whether two parties have the same secret information. Popular instant message cryptography package Off-the-Record Messaging
Off-the-record messaging
Off-the-Record Messaging, commonly referred to as OTR, is a cryptographic protocol that provides strong encryption for instant messaging conversations. OTR uses a combination of the AES symmetric-key algorithm, the Diffie–Hellman key exchange, and the SHA-1 hash function...
uses the Socialist Millionaire protocol for authentication, in which the secrets
 and
and 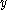 contain information about both parties' long-term authentication public keys, as well as information entered by the users themselves.
contain information about both parties' long-term authentication public keys, as well as information entered by the users themselves.Procedure
All operations are performed modulo a prime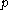 , or in other words, in the multiplicative group
, or in other words, in the multiplicative groupMultiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
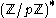 . Let
. Let 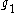 be a generator
be a generatorGenerator
Generator may refer to:* Electrical generator* Engine-generator, an electrical generator, but with its own engine.* Generator , any of several closely related usages in mathematics.Computing:...
of the group (any element other than 1, noting that 0 is not an element of multiplicative groups). The values
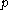 and
and 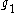 are agreed on before the protocol, and in practice are generally fixed in a given implementation. For example, in Off-the-Record Messaging
are agreed on before the protocol, and in practice are generally fixed in a given implementation. For example, in Off-the-Record Messaging 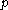 is a specific fixed 1536-bit prime. All sent values include zero-knowledge proofs that they were generated according to this protocol, as indicated in the detailed description below.
is a specific fixed 1536-bit prime. All sent values include zero-knowledge proofs that they were generated according to this protocol, as indicated in the detailed description below.Assuming that Alice begins the exchange:
- Alice:
- Picks random exponents
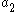 and
and 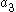
- Sends Bob
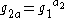 and
and 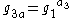
- Picks random exponents
- Bob:
- Picks random exponents
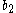 and
and 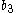
- Computes
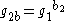 and
and 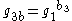
- Computes
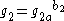 and
and 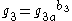
- Picks a random exponent

- Computes
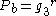 and
and 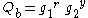
- Sends Alice
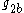 ,
, 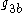 ,
, 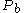 and
and 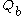
- Picks random exponents
- Alice:
- Computes
 and
and 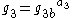
- (
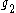 and
and 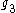 have effectively been negotiated via the Diffie-Hellman key exchangeDiffie-Hellman key exchangeDiffie–Hellman key exchange Synonyms of Diffie–Hellman key exchange include:*Diffie–Hellman key agreement*Diffie–Hellman key establishment*Diffie–Hellman key negotiation...
have effectively been negotiated via the Diffie-Hellman key exchangeDiffie-Hellman key exchangeDiffie–Hellman key exchange Synonyms of Diffie–Hellman key exchange include:*Diffie–Hellman key agreement*Diffie–Hellman key establishment*Diffie–Hellman key negotiation...
.)
- (
- Picks a random exponent

- Computes
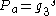 and
and 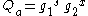
- Computes
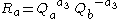
- Sends Bob
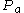 ,
, 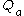 and
and 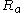
- Computes
- Bob:
- Computes
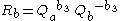
- Computes
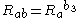
- Checks whether
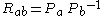
- Sends Alice
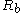
- Computes
- Alice:
- Computes
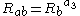
- Checks whether
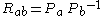
- Computes
The correctness of this algorithm (but not its security) can be shown by simply representing all values in terms of the inputs
 ,
, 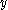 , and
, and 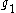 , and the randomly generated values
, and the randomly generated values 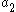 ,
, 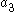 ,
, 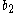 ,
, 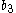 ,
,  , and
, and  :
: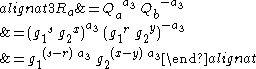
Assuming
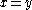 , then
, then 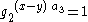 , and therefore
, and therefore 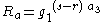 . The same logic holds to show
. The same logic holds to show  . Therefore,
. Therefore,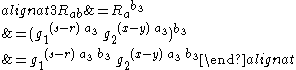
Similarly expanding
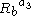 reveals that the values of
reveals that the values of 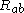 that Alice and Bob generate are identical. Finally, examining the equation being tested by Alice and Bob shows that the algorithm works:
that Alice and Bob generate are identical. Finally, examining the equation being tested by Alice and Bob shows that the algorithm works: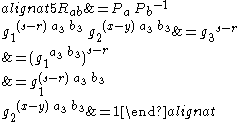
As the last equation given above holds only if
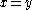 , and as it is equivalent to the first equation, the tests Alice and Bob perform of
, and as it is equivalent to the first equation, the tests Alice and Bob perform of 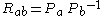 are therefore equivalent to testing
are therefore equivalent to testing 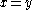 , completing a proof of correctness.
, completing a proof of correctness.However, as written above the protocol is vulnerable to poisoning whereby either Alice or Bob chooses (
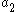 ,
, 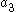 ) or (
) or (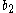 ,
, 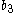 ) to be zero to be able to predict the result http://weizenspr.eu/2009/der-strippende-sozialistische-millionar/. To solve this problem, check that the pairs (
) to be zero to be able to predict the result http://weizenspr.eu/2009/der-strippende-sozialistische-millionar/. To solve this problem, check that the pairs (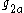 ,
, 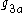 ) and (
) and (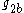 ,
, 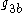 ) are not equal to one.
) are not equal to one.
