Solid Klein bottle
Encyclopedia
In mathematics
, a solid Klein bottle is a 3-manifold
(with boundary) homeomorphic
to the quotient space
obtained by gluing the top of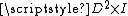
(cylinder) to the bottom by a reflection, i.e. the point 
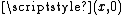is identified with 
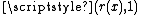where 
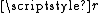is reflection of the disc 
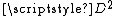across a diameter.
Note the boundary of the solid Klein bottle is a Klein bottle
.
Alternatively, one can visualize the solid Klein bottle as the trivial product
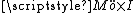, of the möbius strip
and an interval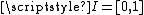
. In this model one can see that
the core central curve at 1/2 has a regular neighborhood which is again a trivial cartesian product
:
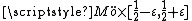and whose boundary is a Klein bottle as previously noticed
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a solid Klein bottle is a 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
(with boundary) homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
obtained by gluing the top of
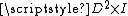(cylinder) to the bottom by a reflection, i.e. the point 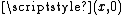is identified with 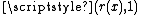where 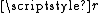is reflection of the disc 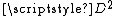across a diameter.Note the boundary of the solid Klein bottle is a Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
.
Alternatively, one can visualize the solid Klein bottle as the trivial product
I-bundle
In mathematics, an I-bundle is a fiber bundle whose fiber is an interval and whose base is a manifold. Any kind of interval, open, closed, semi-open, semi-closed, open-bounded, compact, even rays, can be the fiber....
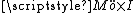, of the möbius stripMöbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
and an interval
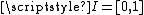. In this model one can see thatthe core central curve at 1/2 has a regular neighborhood which is again a trivial cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
:
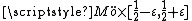and whose boundary is a Klein bottle as previously noticed