Sparse approximation
Encyclopedia
Sparse approximation is the problem of finding a signal or vector estimate with sparseness property, that is having a small number of nonzero elements, that satisfies (approximately) a system of equations.
For example, consider a linear system of equations y = Ax, where A is a real M-by-N matrix
and M < N. In general, this problem is ill-posed as there are infinitely many x that solve this system.
One way to enforce sparsity is to choose x such that as many components as possible are zero. In other words, we want to solve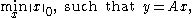
where the objective function is defined by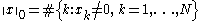
and # denotes the cardinality of the set. However, this problem is NP-complete
because classical combinatorial optimization
can be reduced to it.
For example, consider a linear system of equations y = Ax, where A is a real M-by-N matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and M < N. In general, this problem is ill-posed as there are infinitely many x that solve this system.
One way to enforce sparsity is to choose x such that as many components as possible are zero. In other words, we want to solve
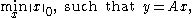
where the objective function is defined by
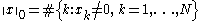
and # denotes the cardinality of the set. However, this problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
because classical combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
can be reduced to it.
Approximations
There are several algorithms that find a suboptimal sparse approximation:- Matching pursuitMatching pursuitMatching pursuit is a type of numerical technique which involves finding the "best matching" projections of multidimensional data onto an over-complete dictionary D...
sets elements of
in a greedy way. - Basis pursuit solves
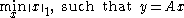instead, using linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
. - The Method Of Frames solves
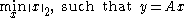. - Dantzig selector