Spectrum continuation analysis
Encyclopedia
Spectrum continuation analysis (SCA) is a generalization of the concept of Fourier series
to non-periodic functions of which only a fragment has been sampled in the time domain.
Recall that a Fourier series is only suitable to the analysis of periodic (or finite-domain) functions f(x) with period 2π. It can be expressed as an infinite series of sinusoids:
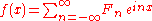
where
is the amplitude of the individual harmonics.
In SCA however, one decomposes the spectrum into optimized discrete frequencies. As a consequence, and as the period of the sampled function is supposed to be infinite or not yet known, each of the discrete periodic functions that compose the sampled function fragment can not be considered to be a multiple of the fundamental frequency:
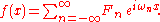
As such, SCA does not necessarily deliver
periodic functions, as would have been the case in Fourier analysis.
For real-valued functions, the SCA series can be written as:
where An and Bn are the series amplitudes. The amplitudes can only be solved if the series of values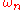
is previously optimized for a desired objective function (usually least residuals
).
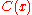is not necessarily the average value over the sampled interval: one might prefer to include predominant information on the behavior of the offset value in the time domain.
) time series fragment. Unlike ordinary Fourier analysis that infinitely repeats an observed function period or time domain, SCA filters the exact composing frequencies out of the observed spectrum and let them continue (resp. precede) in the time domain.
In the scientific terminology, therefore preference is given to the term continuation rather than for instance extrapolation.
Since discrete Fourier transform
is inherently related to Fourier analysis, this type of spectral analysis is by definition not suitable for spectrum decomposition in SCA. DFT (or FFT
) may provide however an initial approximation, which often speeds up the decomposition.
After decomposition of a discrete frequency, it should be filtered for optimal resolution (i.e. varying three parameters: frequency value, amplitude and phase).
(or FFT
), which is characterized by perfect spectral resolution, but poor temporal information, SCA favours temporal information, but yields higher spectrum dispersion. This property shows where the analytic strength of SCA is located. For instance, discrete composing frequency resolution is by definition far better in SCA than in DFT.
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
to non-periodic functions of which only a fragment has been sampled in the time domain.
Recall that a Fourier series is only suitable to the analysis of periodic (or finite-domain) functions f(x) with period 2π. It can be expressed as an infinite series of sinusoids:
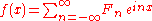
where
is the amplitude of the individual harmonics.In SCA however, one decomposes the spectrum into optimized discrete frequencies. As a consequence, and as the period of the sampled function is supposed to be infinite or not yet known, each of the discrete periodic functions that compose the sampled function fragment can not be considered to be a multiple of the fundamental frequency:
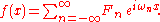
As such, SCA does not necessarily deliver
periodic functions, as would have been the case in Fourier analysis.For real-valued functions, the SCA series can be written as:
where An and Bn are the series amplitudes. The amplitudes can only be solved if the series of values
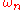is previously optimized for a desired objective function (usually least residualsErrors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
).
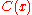is not necessarily the average value over the sampled interval: one might prefer to include predominant information on the behavior of the offset value in the time domain.Etymology
SCA deals with the prediction problem of continuing a frequency spectrum beyond a sampled (usually stochasticStochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
) time series fragment. Unlike ordinary Fourier analysis that infinitely repeats an observed function period or time domain, SCA filters the exact composing frequencies out of the observed spectrum and let them continue (resp. precede) in the time domain.
In the scientific terminology, therefore preference is given to the term continuation rather than for instance extrapolation.
Algorithm
An algorithm is required to cope with several problems: detrending, decomposition, frequency resolution optimization, superposition, transformation and computational efficiency.- Detrending or trend estimation.
- Decomposition.
Since discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
is inherently related to Fourier analysis, this type of spectral analysis is by definition not suitable for spectrum decomposition in SCA. DFT (or FFT
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
) may provide however an initial approximation, which often speeds up the decomposition.
- Improving frequency resolution.
After decomposition of a discrete frequency, it should be filtered for optimal resolution (i.e. varying three parameters: frequency value, amplitude and phase).
- Transformation.
Spectrum dispersion
Compared to DFTDFT
DFT may stand for:*Discrete Fourier transform*Decision field theory*Density functional theory*Demand Flow Technology*The United Kingdom's Department for Transport*Design For Test*Deareating Feed Tank*Digital Film Technology maker of the Spirit DataCine...
(or FFT
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
), which is characterized by perfect spectral resolution, but poor temporal information, SCA favours temporal information, but yields higher spectrum dispersion. This property shows where the analytic strength of SCA is located. For instance, discrete composing frequency resolution is by definition far better in SCA than in DFT.