
Spherical image
Encyclopedia
In differential geometry, the spherical image of a unit-speed curve is given by taking the curve's tangent vector
s as points, all of which must lie on the unit sphere
. The movement of the spherical image describes the changes in the original curve's direction If is a unit-speed curve, that is
is a unit-speed curve, that is  , and
, and  is the unit tangent vector field along
is the unit tangent vector field along  , then the curve
, then the curve 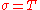 is the spherical image of
is the spherical image of  . All points of
. All points of  must lie on the unit sphere because
must lie on the unit sphere because 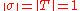 .
.
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s as points, all of which must lie on the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
. The movement of the spherical image describes the changes in the original curve's direction If
 is a unit-speed curve, that is
is a unit-speed curve, that is  , and
, and  is the unit tangent vector field along
is the unit tangent vector field along  , then the curve
, then the curve 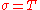 is the spherical image of
is the spherical image of  . All points of
. All points of  must lie on the unit sphere because
must lie on the unit sphere because 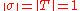 .
.

