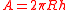Spherical segment
Encyclopedia
In geometry
, a spherical segment is the solid defined by cutting a sphere
with a pair of parallel planes
.
It can be thought of as a spherical cap
with the top truncated, and so it corresponds to a spherical frustum
. The surface
of the spherical segment (excluding the bases) is called spherical zone.
If the radius
of the sphere is called r, the radius of the spherical segment bases a and b, and the height of the segment (the distance from one parallel plane to the other) called h, the volume
of the spherical segment is then:

The area
of the spherical zone —which excludes the top and bottom bases— is given by: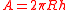
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a spherical segment is the solid defined by cutting a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
with a pair of parallel planes
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
.
It can be thought of as a spherical cap
Spherical cap
In geometry, a spherical cap is a portion of a sphere cut off by a plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere....
with the top truncated, and so it corresponds to a spherical frustum
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
. The surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
of the spherical segment (excluding the bases) is called spherical zone.
If the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the sphere is called r, the radius of the spherical segment bases a and b, and the height of the segment (the distance from one parallel plane to the other) called h, the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of the spherical segment is then:

The area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the spherical zone —which excludes the top and bottom bases— is given by: