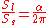Spherical wedge
Encyclopedia
In geometry
, a spherical wedge or ungula is a portion of a ball
bounded by two plane semidisks and a spherical lune (termed the wedge's base). The angle between the radii lying within the bounding semidisks is the dihedral
angle of the wedge α. If AB is a semidisk that forms a ball when completely revolved about the z-axis, revolving AB only through a given α produces a spherical wedge of the same angle α. Beman (2008) remarks that "a spherical wedge is to the sphere of which it is a part as the angle of the wedge is to a perigon." A spherical wedge of α = π radian
s (180°) is called a hemisphere
, while a spherical wedge of α = 2π radians (360°) constitutes a complete ball.
The volume
of a spherical wedge can be intuitively related to the AB definition in that while the volume of a ball of radius r is given by ,
,
the volume a spherical wedge of the same radius r is given by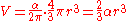
Extrapolating the same principle and considering that the surface area of a sphere is given by , it can be seen that the surface area of the lune corresponding to the same wedge is given by
, it can be seen that the surface area of the lune corresponding to the same wedge is given by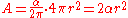
Hart (2009) states that the "volume of a spherical wedge is to the volume of the sphere as the number of degree
s in the [angle of the wedge] is to 360". Hence, and through derivation of the spherical wedge volume formula, it can be concluded that, if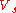 is the volume of the sphere and
is the volume of the sphere and 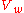 is the volume of a given spherical wedge,
is the volume of a given spherical wedge,
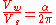
Also, if Sl is the area
of a given wedge's lune, and Ss is the area of the wedge's sphere,
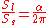
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a spherical wedge or ungula is a portion of a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
bounded by two plane semidisks and a spherical lune (termed the wedge's base). The angle between the radii lying within the bounding semidisks is the dihedral
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
angle of the wedge α. If AB is a semidisk that forms a ball when completely revolved about the z-axis, revolving AB only through a given α produces a spherical wedge of the same angle α. Beman (2008) remarks that "a spherical wedge is to the sphere of which it is a part as the angle of the wedge is to a perigon." A spherical wedge of α = π radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s (180°) is called a hemisphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, while a spherical wedge of α = 2π radians (360°) constitutes a complete ball.
The volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a spherical wedge can be intuitively related to the AB definition in that while the volume of a ball of radius r is given by
 ,
,the volume a spherical wedge of the same radius r is given by
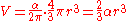
Extrapolating the same principle and considering that the surface area of a sphere is given by
 , it can be seen that the surface area of the lune corresponding to the same wedge is given by
, it can be seen that the surface area of the lune corresponding to the same wedge is given by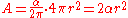
Hart (2009) states that the "volume of a spherical wedge is to the volume of the sphere as the number of degree
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
s in the [angle of the wedge] is to 360". Hence, and through derivation of the spherical wedge volume formula, it can be concluded that, if
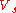 is the volume of the sphere and
is the volume of the sphere and 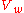 is the volume of a given spherical wedge,
is the volume of a given spherical wedge,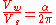
Also, if Sl is the area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of a given wedge's lune, and Ss is the area of the wedge's sphere,