
Spigot algorithm
Encyclopedia
A spigot algorithm is a type of algorithm
used to compute the value of a mathematical constant such as π
or e
. Unlike recursive
algorithms, a spigot algorithm yields digits incrementally without using previously computed digits. The Bailey-Borwein-Plouffe formula for the binary digits of π is an example of a spigot algorithm.
of 2 using the identity

To start calculating binary digits from, say, the 8th place we multiply this identity by 27:
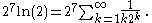
We then divide the infinite sum into a "head", in which the exponents of 2 are greater than or equal to zero, and a "tail", in which the exponents of 2 are negative:
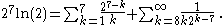
We are only interested in the fractional part of this value, so we can replace each of the summands in the "head" by
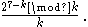
Calculating each of these terms and adding them to a running total where we again only keep the fractional part, we have:
We add a few terms in the "tail", noting that the error introduced by truncating the sum is less than the final term:
Adding the "head" and the first few terms of the "tail" together we get:
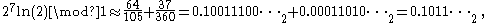
so the 8th to 11th binary digits in the binary expansion of ln(2) are 1, 0, 1, 1. Note that we have not calculated the values of the first 7 binary digits - indeed, all information about them has been intentionally discarded by using modular arithmetic
in the "head" sum.
The same approach can be used to calculate digits of the binary expansion of ln(2) starting from an arbitrary nth position. The number of terms in the "head" sum increases linearly with n, but the complexity of each term only increases with the logarithm of n if an efficient method of modular exponentiation
is used. The precision
of calculations and intermediate results and the number of terms taken from the "tail" sum are all independent of n, and only depend on the number of binary digits that are being calculated - single precision arithmetic can be used to calculate around 12 binary digits, regardless of the starting position.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
used to compute the value of a mathematical constant such as π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
or e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
. Unlike recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
algorithms, a spigot algorithm yields digits incrementally without using previously computed digits. The Bailey-Borwein-Plouffe formula for the binary digits of π is an example of a spigot algorithm.
Example
This example illustrates the working of a spigot algorithm by calculating the binary digits of the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of 2 using the identity

To start calculating binary digits from, say, the 8th place we multiply this identity by 27:
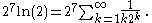
We then divide the infinite sum into a "head", in which the exponents of 2 are greater than or equal to zero, and a "tail", in which the exponents of 2 are negative:
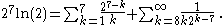
We are only interested in the fractional part of this value, so we can replace each of the summands in the "head" by
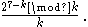
Calculating each of these terms and adding them to a running total where we again only keep the fractional part, we have:
| k | A = 27-k | B = A mod k | C = B / k | Sum of C mod 1 |
|---|---|---|---|---|
| 1 | 64 | 0 | 0 | 0 |
| 2 | 32 | 0 | 0 | 0 |
| 3 | 16 | 1 | 1/3 | 1/3 |
| 4 | 8 | 0 | 0 | 1/3 |
| 5 | 4 | 4 | 4/5 | 2/15 |
| 6 | 2 | 2 | 1/3 | 7/15 |
| 7 | 1 | 1 | 1/7 | 64/105 |
We add a few terms in the "tail", noting that the error introduced by truncating the sum is less than the final term:
| k | D = 1/k2k-7 | Sum of D | Maximum error |
|---|---|---|---|
| 8 | 1/16 | 1/16 | 1/16 |
| 9 | 1/36 | 13/144 | 1/36 |
| 10 | 1/80 | 37/360 | 1/80 |
Adding the "head" and the first few terms of the "tail" together we get:
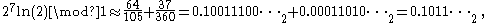
so the 8th to 11th binary digits in the binary expansion of ln(2) are 1, 0, 1, 1. Note that we have not calculated the values of the first 7 binary digits - indeed, all information about them has been intentionally discarded by using modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
in the "head" sum.
The same approach can be used to calculate digits of the binary expansion of ln(2) starting from an arbitrary nth position. The number of terms in the "head" sum increases linearly with n, but the complexity of each term only increases with the logarithm of n if an efficient method of modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
is used. The precision
Precision (arithmetic)
The precision of a value describes the number of digits that are used to express that value. In a scientific setting this would be the total number of digits or, less commonly, the number of fractional digits or decimal places...
of calculations and intermediate results and the number of terms taken from the "tail" sum are all independent of n, and only depend on the number of binary digits that are being calculated - single precision arithmetic can be used to calculate around 12 binary digits, regardless of the starting position.

