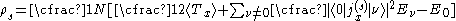Spin stiffness
Encyclopedia
The spin-stiffness or spin rigidity or helicity modulus or the "superfluid density" (for bosons the superfluid density is proportional to the spin stiffness) is a constant which represents the change in the ground state energy of a spin system as a result of introducing a slow in plane twist of the spins. The importance of this constant is in its use as an indicator of quantum phase transitions-- specifically in models with metal-insulator transitions such as Mott insulators. It is also related to other topological invariants such as the Berry phase and Chern numbers as in the Quantum hall effect.
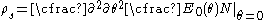
where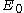
is the ground state energy, 
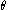is the twisting angle, and N is the number of lattice sites.
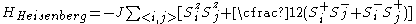
Now we introduce a rotation in the system at site i by an angle θi around the z-axis:
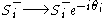
Plugging these back into the Heisenberg Hamiltonian:
now let θij = θi - θj and expand around θij = 0 via a MacLaurin expansion
only keeping terms up to second order in θij
where the first term is independent of θ and the second term is a perturbation
for small θ.
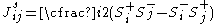is the z-component of the spin current operator
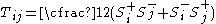is the "spin kinetic energy"
Consider now the case of identical twists, θx only that exist along nearest neighbor bonds along the x-axis
Then since the spin stiffness is related to the difference in the ground state energy by
then for small θx and with the help of second order perturbation theory
we get:
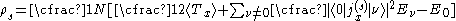
Mathematically
Mathematically it can be defined by the following equation: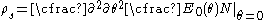where
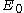is the ground state energy, 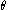is the twisting angle, and N is the number of lattice sites.Spin stiffness of the Heisenberg model
Start off with the simple Heisenberg spin Hamiltonian: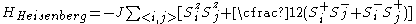Now we introduce a rotation in the system at site i by an angle θi around the z-axis:
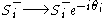
Plugging these back into the Heisenberg Hamiltonian:
now let θij = θi - θj and expand around θij = 0 via a MacLaurin expansion
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
only keeping terms up to second order in θij
where the first term is independent of θ and the second term is a perturbation
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
for small θ.
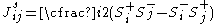is the z-component of the spin current operator 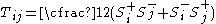is the "spin kinetic energy"Consider now the case of identical twists, θx only that exist along nearest neighbor bonds along the x-axis
Then since the spin stiffness is related to the difference in the ground state energy by
then for small θx and with the help of second order perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
we get: