
Spring (math)
Encyclopedia
In geometry
, a spring is a surface in the shape of a coiled tube, generated by sweeping a circle
about the path of a helix
.



where

 is the distance from the center of the tube to the center of the helix
is the distance from the center of the tube to the center of the helix
, is the radius of the tube,
is the radius of the tube,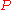 is the speed of the movement along the z axis (in a right-handed
is the speed of the movement along the z axis (in a right-handed
Cartesian coordinate system
, positive values create right-handed springs, whereas negative values create left-handed springs), is the number of rounds in circle.
is the number of rounds in circle.
The implicit function
in Cartesian coordinates for a spring wrapped around the z-axis, with = 1 is
= 1 is

The interior volume
of the spiral is given by

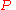 and the incline of the tube).
and the incline of the tube).
An alternative would be to have a circular cross section in the plane perpendicular to the helix curve. This would be closer to the shape of a physical spring. The mathematics would be much more complicated.
The torus
can be viewed as a special case of the spring obtained when the helix degenerates to a circle.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a spring is a surface in the shape of a coiled tube, generated by sweeping a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
about the path of a helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
.
Definition
A spring wrapped around the z-axis can be defined parametrically by:


where


 is the distance from the center of the tube to the center of the helix
is the distance from the center of the tube to the center of the helixHelix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
,
 is the radius of the tube,
is the radius of the tube,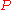 is the speed of the movement along the z axis (in a right-handed
is the speed of the movement along the z axis (in a right-handedRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, positive values create right-handed springs, whereas negative values create left-handed springs),
 is the number of rounds in circle.
is the number of rounds in circle.The implicit function
Implicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
in Cartesian coordinates for a spring wrapped around the z-axis, with
 = 1 is
= 1 is
The interior volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of the spiral is given by

Other definitions
Note that the previous definition uses a vertical circular cross section. This is not entirely accurate as the tube becomes increasingly distorted as the Torsion increases (ratio of the speed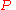 and the incline of the tube).
and the incline of the tube).An alternative would be to have a circular cross section in the plane perpendicular to the helix curve. This would be closer to the shape of a physical spring. The mathematics would be much more complicated.
The torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
can be viewed as a special case of the spring obtained when the helix degenerates to a circle.

