Standard conjectures on algebraic cycles
Encyclopedia
In mathematics
, the standard conjectures about algebraic cycles is a package of several conjecture
s describing the relationship of algebraic cycle
s and Weil cohomology theories
. One of the original applications of these conjectures, envisaged by Alexander Grothendieck
, was to prove that his construction of pure motives
gave an abelian category
that is semisimple. Moreover, as he pointed out, the standard conjectures also imply the hardest part of the Weil conjectures
, namely the "Riemann hypothesis" conjecture that remained open at the end of the 1960s and was proved later by Pierre Deligne
; for details on the link between Weil and standard conjectures, see . The standard conjectures remain open problems, so that their application gives only conditional proof
s of results. In quite a few cases, including that of the Weil conjectures, other methods have been found to prove such results unconditionally.
The classical formulations of the standard conjectures involve a fixed Weil cohomology theory H. All of the conjectures deal with "algebraic" cohomology classes, which means a morphism on the cohomology of a smooth projective variety
induced by an algebraic cycle with rational coefficients on the product X × X via the cycle class map (which is part of the structure of a Weil cohomology theory).
for H some hyperplane in the ambient projective space PN containing the given smooth projective variety X, the Lefschetz operator
which is defined by intersecting cohomology classes with W gives an isomorphism
Define
be the composition
and
by
The Lefschetz conjecture states that the Lefschetz operator Λ is induced by an algebraic cycle.
).
The conjecture is known to hold for curves, surfaces and abelian varieties.
. It states the positive definiteness of the cup product pairing on primitive algebraic cohomology classes. If it holds, then the Lefschetz conjecture implies Conjecture D. In characteristic zero the Hodge standard conjecture holds, being a consequence of Hodge theory
. In positive characteristic the Hodge standard conjecture is known only for surfaces and abelian varieties.
The Hodge standard conjecture is not to be confused with the Hodge conjecture
which states that for smooth projective varieties over C, every rational (p,p)-class is algebraic. The Hodge conjecture implies the Lefschetz conjecture and conjecture D for varieties over fields of characteristic zero. Likewise for fields of finite characteristic the Tate conjectures in ℓ-adic cohomology
imply the Lefschetz conjecture.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the standard conjectures about algebraic cycles is a package of several conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
s describing the relationship of algebraic cycle
Algebraic cycle
In mathematics, an algebraic cycle on an algebraic variety V is, roughly speaking, a homology class on V that is represented by a linear combination of subvarieties of V. Therefore the algebraic cycles on V are the part of the algebraic topology of V that is directly accessible in algebraic geometry...
s and Weil cohomology theories
Weil cohomology theory
In algebraic geometry, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil...
. One of the original applications of these conjectures, envisaged by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, was to prove that his construction of pure motives
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
gave an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
that is semisimple. Moreover, as he pointed out, the standard conjectures also imply the hardest part of the Weil conjectures
Weil conjectures
In mathematics, the Weil conjectures were some highly-influential proposals by on the generating functions derived from counting the number of points on algebraic varieties over finite fields....
, namely the "Riemann hypothesis" conjecture that remained open at the end of the 1960s and was proved later by Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
; for details on the link between Weil and standard conjectures, see . The standard conjectures remain open problems, so that their application gives only conditional proof
Conditional proof
A conditional proof is a proof that takes the form of asserting a conditional, and proving that the antecedent of the conditional necessarily leads to the consequent....
s of results. In quite a few cases, including that of the Weil conjectures, other methods have been found to prove such results unconditionally.
The classical formulations of the standard conjectures involve a fixed Weil cohomology theory H. All of the conjectures deal with "algebraic" cohomology classes, which means a morphism on the cohomology of a smooth projective variety
- H*(X) → H*(X)
induced by an algebraic cycle with rational coefficients on the product X × X via the cycle class map (which is part of the structure of a Weil cohomology theory).
Lefschetz type standard conjecture
Lefschetz type standard conjecture, also called conjecture B: One of the axioms of a Weil theory is the so-called hard Lefschetz theorem (or axiom): for a fixed smooth hyperplane sectionHyperplane section
In mathematics, a hyperplane section of a subset X of projective space Pn is the intersection of X with some hyperplane H — in other words we look at the subset XH of those elements x of X that satisfy the single linear condition L = 0 defining H as a linear subspace...
- W = H ∩ X,
for H some hyperplane in the ambient projective space PN containing the given smooth projective variety X, the Lefschetz operator
- L : Hi(X) → Hi+2,
which is defined by intersecting cohomology classes with W gives an isomorphism
- Ln-i: Hi(X) → H2n-i(X) (i ≦ n = dim X).
Define
- Λ : Hi(X) → Hi-2(X) for 'i ≦ n
be the composition
- (Ln-i+2)-1
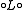(Ln-i)-1
and
- Λ : H2n-i+2(X) → H2n-i(X)
by
- (Ln-i)
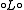(Ln-i+2)-1 -1.
The Lefschetz conjecture states that the Lefschetz operator Λ is induced by an algebraic cycle.
Künneth type standard conjecture
The Lefschetz conjecture implies the Künneth type standard conjecture, also called conjecture C: It is conjectured that the projectors H∗(X) ↠ Hi(X) ↣ H∗(X) are algebraic, i.e. induced by a cycle πi ⊂ X × X with rational coefficients. This implies that every pure motive M decomposes in graded pieces of pure weights (see motivesMotive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
).
The conjecture is known to hold for curves, surfaces and abelian varieties.
Conjecture D (numerical equivalence vs. homological equivalence)
Conjecture D states that numerical equivalence and homological equivalence agree. (It implies in particular the latter does not depend on the choice of the Weil cohomology theory). This conjecture implies the Lefschetz conjecture. If the Hodge standard conjecture holds, then the Lefschetz conjecture and Conjecture D are equivalent.The Hodge standard conjecture
The Hodge standard conjecture is modelled on the Hodge index theoremHodge index theorem
In mathematics, the Hodge index theorem for an algebraic surface V determines the signature of the intersection pairing on the algebraic curves C on V...
. It states the positive definiteness of the cup product pairing on primitive algebraic cohomology classes. If it holds, then the Lefschetz conjecture implies Conjecture D. In characteristic zero the Hodge standard conjecture holds, being a consequence of Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
. In positive characteristic the Hodge standard conjecture is known only for surfaces and abelian varieties.
The Hodge standard conjecture is not to be confused with the Hodge conjecture
Hodge conjecture
The Hodge conjecture is a major unsolved problem in algebraic geometry which relates the algebraic topology of a non-singular complex algebraic variety and the subvarieties of that variety. More specifically, the conjecture says that certain de Rham cohomology classes are algebraic, that is, they...
which states that for smooth projective varieties over C, every rational (p,p)-class is algebraic. The Hodge conjecture implies the Lefschetz conjecture and conjecture D for varieties over fields of characteristic zero. Likewise for fields of finite characteristic the Tate conjectures in ℓ-adic cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
imply the Lefschetz conjecture.