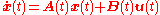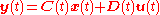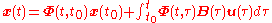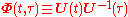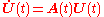State-transition matrix
Encyclopedia
In control theory
, the state-transition matrix is a matrix whose product with the state vector
at an initial time 
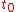gives 
at a later time 
. The state-transition matrix can be used to obtain the general solution of linear dynamical systems. It is also known as the matrix exponential
.
model
The general solution is given by
The state-transition matrix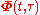
, given by
where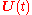
is the fundamental solution matrix that satisfies
is a
matrix that is a linear mapping onto itself, i.e., with 
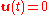, given the state 
at any time 
, the state at any other time 
is given by the mapping
While the state transition matrix φ is not completely unknown, it must always satisfy the following relationships:
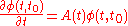and
for all 
and where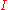 
is the identity matrix
.
And φ also must have the following properties:
If the system is time-invariant, we can define φ as:
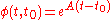
In the time-variant case, there are many different functions that may satisfy these requirements, and the solution is dependent on the structure of the system. The state-transition matrix must be determined before analysis on the time-varying solution can continue.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, the state-transition matrix is a matrix whose product with the state vector
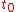at an initial time gives at a later time . The state-transition matrix can be used to obtain the general solution of linear dynamical systems. It is also known as the matrix exponentialMatrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
.
Overview
Consider the general linear state spaceState space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
model
The general solution is given by
The state-transition matrix
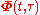, given by
where
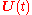is the fundamental solution matrix that satisfies
is a
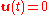matrix that is a linear mapping onto itself, i.e., with , given the state at any time , the state at any other time is given by the mappingWhile the state transition matrix φ is not completely unknown, it must always satisfy the following relationships:
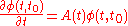and for all and where 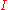is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
And φ also must have the following properties:
| 1. |  |
| 2. |  |
| 3. |  |
| 4. |  |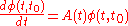
If the system is time-invariant, we can define φ as:
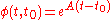
In the time-variant case, there are many different functions that may satisfy these requirements, and the solution is dependent on the structure of the system. The state-transition matrix must be determined before analysis on the time-varying solution can continue.