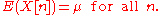Stationary sequence
Encyclopedia
In probability theory
– specifically in the theory of stochastic process
es, a stationary sequence is a random sequence
whose joint probability distribution is invariant
over time. If a random sequence X j is stationary then the following holds:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
– specifically in the theory of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, a stationary sequence is a random sequence
Random sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let X1,...,Xn be independent random variables...". Yet as D. H. Lehmer stated in...
whose joint probability distribution is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
over time. If a random sequence X j is stationary then the following holds:
-
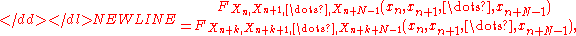
where F is the joint cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s in the subscript.
If a sequence is stationary then it is wide-sense stationary.
If a sequence is stationary then it has a constant mean (which may not be finite):
-