Stern prime
Encyclopedia
A Stern prime, named for Moritz Abraham Stern
, is a prime number
that is not the sum of a smaller prime and twice the square of a nonzero integer
. Or, to put it algebraically, if for a prime q there is no smaller prime p and nonzero integer b such that q = p + 2b², then q is a Stern prime. The known Stern primes are
So, for example, if we try subtracting from 137 the first few squares doubled in order, we get {135, 129, 119, 105, 87, 65, 39, 9}, none of which is prime. That means that 137 is a Stern prime. On the other hand, 139 is not a Stern prime, since we can express it as 137 + 2(1²), or 131 + 2(2²), etc.
In fact, many primes have more than one representation of this sort. Given a twin prime
, the larger prime of the pair has, if nothing else, a Goldbach representation of p + 2(1²). And if that prime is the largest of a prime quadruplet, p + 8, then p + 2(2²) is also available. Sloane's lists odd numbers with at least n Goldbach representations. Leonhard Euler
observed that as the numbers get larger, they get more representations of the form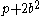
, suggesting that there might be a largest number with zero such representations.
Therefore, the above list of Stern primes might be not only finite, but also complete. According to Jud McCranie, these are the only Stern primes from among the first 100000 primes. All the known Stern primes have more efficient Waring representation
s than their Goldbach representations would suggest.
Christian Goldbach
conjectured in a letter to Leonhard Euler that every odd integer is of the form p + 2b² with b allowed to be any integer, including zero. Laurent Hodges believes that Stern became interested in the problem after reading a book of Goldbach's correspondence. Because in Stern's time, 1 was considered a prime, 3 was not a Stern prime because it could be represented as 1 + 2(1²). The rest of the list remains the same.
Moritz Abraham Stern
Moritz Abraham Stern was a German mathematician. Stern became Ordinarius at Göttingen University in 1858, succeeding Carl Friedrich Gauss. Stern was the first Jewish full professor at a German university....
, is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
that is not the sum of a smaller prime and twice the square of a nonzero integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. Or, to put it algebraically, if for a prime q there is no smaller prime p and nonzero integer b such that q = p + 2b², then q is a Stern prime. The known Stern primes are
- 2, 3, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 137137 (number)137 is the natural number following 136 and preceding 138.-In mathematics :One hundred [and] thirty-seven is the 33rd prime number; the next is 139, with which it comprises a twin prime, and thus 137 is a Chen prime. 137 is an Eisenstein prime with no imaginary part and a real part of the form 3n -...
, 227227 (number)227 is the natural number between 226 and 228. It is also a prime number.-In mathematics:227 is a prime number, and a twin prime with 229 . 223 plus 4 is 227, so they are cousin primes...
, 977, 1187, 1493 .
So, for example, if we try subtracting from 137 the first few squares doubled in order, we get {135, 129, 119, 105, 87, 65, 39, 9}, none of which is prime. That means that 137 is a Stern prime. On the other hand, 139 is not a Stern prime, since we can express it as 137 + 2(1²), or 131 + 2(2²), etc.
In fact, many primes have more than one representation of this sort. Given a twin prime
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
, the larger prime of the pair has, if nothing else, a Goldbach representation of p + 2(1²). And if that prime is the largest of a prime quadruplet, p + 8, then p + 2(2²) is also available. Sloane's lists odd numbers with at least n Goldbach representations. Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
observed that as the numbers get larger, they get more representations of the form
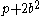, suggesting that there might be a largest number with zero such representations.Therefore, the above list of Stern primes might be not only finite, but also complete. According to Jud McCranie, these are the only Stern primes from among the first 100000 primes. All the known Stern primes have more efficient Waring representation
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
s than their Goldbach representations would suggest.
Christian Goldbach
Christian Goldbach
Christian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...
conjectured in a letter to Leonhard Euler that every odd integer is of the form p + 2b² with b allowed to be any integer, including zero. Laurent Hodges believes that Stern became interested in the problem after reading a book of Goldbach's correspondence. Because in Stern's time, 1 was considered a prime, 3 was not a Stern prime because it could be represented as 1 + 2(1²). The rest of the list remains the same.