Stirling's approximation
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
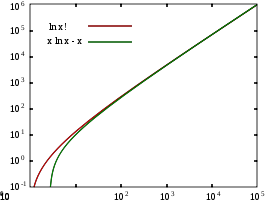
, Stirling's approximation (or Stirling's formula) is an approximation for large factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s. It is named after James Stirling
James Stirling (mathematician)
James Stirling was a Scottish mathematician. The Stirling numbers and Stirling's approximation are named after him.-Biography:...
.
The formula as typically used in applications is
The next term in the O(log(n)) is ln(2πn); a more precise variant of the formula
Asymptotic formula
In mathematics, an asymptotic formula for a quantity depending on natural numbers, or on a variable taking real numbers as values, is a function of natural numbers, or of a real variable, whose values are nearly equal to the values of the former when both are evaluated for the same large values...
is therefore
often written
If we want the approximation for natural logarithm we get:
Derivation
The formula, together with precise estimates of its error, can be derived as follows. Instead of approximating n!, one considers its natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
as this is a slowly varying function:
The right-hand side of this equation is (almost) the approximation by the trapezoid rule of the integral
and the error in this approximation is given by the Euler–Maclaurin formula:
where Bk is a Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
and Rm,n is the remainder term in the Euler–Maclaurin formula.
Take limits to find that
Denote this limit by y. Because the remainder Rm,n in the Euler–Maclaurin formula satisfies
where we use Big-O notation, combining the equations above yields the approximation formula in its logarithmic form:
Taking the exponential of both sides, and choosing any positive integer m, we get a formula involving an unknown quantity ey.
For m=1, the formula is
The quantity ey can be found by taking the limit on both sides as n tends to infinity and using Wallis' product,
which shows that
. Therefore, we get Stirling's formula:
The formula may also be obtained by repeated integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, and the leading term can be found through Laplace's method.
Stirling's formula, without the factor
that is often irrelevant in applications, can be quickly obtained by approximating the sum
with an integral:
Speed of convergence and error estimates
with
Stirling's formula is in fact the first approximation to the following series (now called the Stirling series):
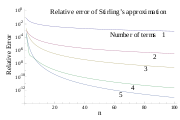
The first graph in this section shows the relative error vs. n, for 1 through all 5 terms listed above.
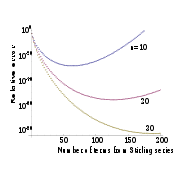
, the error in the truncated series is asymptotically equal to the first omitted term. This is an example of an asymptotic expansionAsymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
. It is not a convergent series; for any particular value of n there are only so many terms of the series that improve accuracy, after which point accuracy actually gets worse. This is demonstrated in the next graph, which shows the relative error vs. the number of terms in the series.
(More precisely, let
be the Stirling series to t terms evaluated at n. The graphs show 
, which, when small, is essentially the relative error.)The asymptotic expansion of the logarithm is also called Stirling's series:
In this case, it is known that the error in truncating the series is always of the same sign and at most the same magnitude as the first omitted term.
Stirling's formula for the Gamma function
For all positive integers,
However, the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, unlike the factorial, is more broadly defined for all complex numbers other than non-positive integers; nevertheless, Stirling's formula may still be applied. If
then
Repeated integration by parts gives
where Bn is the nth Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
(note that the infinite sum is non converging, so this formula is just an asymptotic expansion). The formula is valid for z large enough in absolute value when
, where ε is positive, with an error term of
when the first m terms are used. The corresponding approximation may now be written:
A convergent version of Stirling's formula
Thomas BayesThomas Bayes
Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
showed, in a letter to John Canton
John Canton
John Canton FRS was an English physicist.Canton was born in Middle Street Stroud, Gloucestershire, the son of a weaver John Canton and Esther He had only a common education, after which he was put apprentice to a broadcloth weaver, but his leisure hours were devoted to mathematical studies, and...
published by the Royal Society
Royal Society
The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...
in 1763, that Stirling's formula did not give a convergent series.
Obtaining a convergent version of Stirling's formula entails evaluating
One way to do this is by means of a convergent series of inverted rising exponentials. If
, then
where
where
denotes the Stirling numbers of the first kindStirling numbers of the first kind
In mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...
. From this we obtain a version of Stirling's series
which converges when
.A version suitable for calculators
The approximation:
or equivalently,
can be obtained by rearranging Stirling's extended formula and observing a coincidence between the resultant power series and the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion of the hyperbolic sine function. This approximation is good to more than 8 decimal digits for z with a real part greater than 8. Robert H. Windschitl suggested it in 2002 for computing the Gamma function with fair accuracy on calculators with limited program or register memory (see link 'Toth').
Gergő Nemes proposed in 2007 an approximation which gives the same number of exact digits as the Windschitl approximation but is much simpler:
or equivalently,
History
The formula was first discovered by Abraham de MoivreAbraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
in the form
De Moivre gave an expression for the constant in terms of its natural logarithm.
Stirling's contribution consisted of showing that the constant
is
. The more precise versions are due toJacques Binet.