Stochastic drift
Encyclopedia
In probability theory
, stochastic drift is the change of the average value of a stochastic (random) process
. A related term is the drift rate which is the rate at which the average changes. This is in contrast to the random fluctuations about this average value. For example, the process which counts the number of heads in a series of
coin tosses has a drift rate of 1/2 per toss.
, a cyclical component often fitted by an analysis based on autocorrelation
s or on a Fourier series
, and a random component (stochastic drift) to be removed.
In the course of the time series analysis, identification of cyclical and stochastic drift components is often attempted by alternating autocorrelation analysis and differencing of the trend. Autocorrelation analysis helps to identify the correct phase of the fitted model while the successive differencing transforms the stochastic drift component into white noise
.
Stochastic drift can also occur in population genetics
where it is known as Genetic drift
. A finite population of randomly-reproducing organisms would experience changes from generation to generation in the frequencies of the different genotypes. This may lead to the fixation of one of the genotypes, and even the emergence of a new species
. In sufficiently small populations, drift can also neutralize the effect of deterministic natural selection
on the population.
, etc. — generally evolve stochastically and frequently are non-stationary
. They are typically modelled as either trend stationary or difference stationary
. A trend stationary process {yt} evolves according to
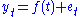
where t is time, f is a deterministic function, and et is a zero-long-run-mean stationary random variable. In this case the stochastic drift can be removed from the data by regressing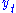
on 
using a functional form coinciding with that of f, and retaining the residuals. In contrast, a unit root (difference stationary) process evolves according to
where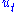
is a zero-long-run-mean stationary random variable; here c is a non-stochastic drift parameter: in the absence of the random shocks ut, the mean of the process would change by c per period. In this case the non-stationarity can be removed from the data by first differencing, and the differenced variable 
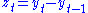will have a mean of c and hence no drift.
In the context of monetary policy
, one policy question is whether a central bank should attempt to achieve a fixed growth rate of the price level
from its current level in each time period, or whether to target a return of the price level to a predetermined growth path. In the latter case no price level drift is allowed away from the predetermined path, while in the former case any stochastic change to the price level permanently affects the expected values of the price level at each time along its future path. In either case the price level has drift in the sense of a rising expected value, but the cases differ according to the type of non-stationarity: difference stationarity in the former case, but trend stationarity in the latter case.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, stochastic drift is the change of the average value of a stochastic (random) process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
. A related term is the drift rate which is the rate at which the average changes. This is in contrast to the random fluctuations about this average value. For example, the process which counts the number of heads in a series of
coin tosses has a drift rate of 1/2 per toss.Stochastic drifts in population studies
Longitudinal studies of secular events are frequently conceptualized as consisting of a trend component fitted by a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, a cyclical component often fitted by an analysis based on autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
s or on a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, and a random component (stochastic drift) to be removed.
In the course of the time series analysis, identification of cyclical and stochastic drift components is often attempted by alternating autocorrelation analysis and differencing of the trend. Autocorrelation analysis helps to identify the correct phase of the fitted model while the successive differencing transforms the stochastic drift component into white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.
Stochastic drift can also occur in population genetics
Population genetics
Population genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
where it is known as Genetic drift
Genetic drift
Genetic drift or allelic drift is the change in the frequency of a gene variant in a population due to random sampling.The alleles in the offspring are a sample of those in the parents, and chance has a role in determining whether a given individual survives and reproduces...
. A finite population of randomly-reproducing organisms would experience changes from generation to generation in the frequencies of the different genotypes. This may lead to the fixation of one of the genotypes, and even the emergence of a new species
Speciation
Speciation is the evolutionary process by which new biological species arise. The biologist Orator F. Cook seems to have been the first to coin the term 'speciation' for the splitting of lineages or 'cladogenesis,' as opposed to 'anagenesis' or 'phyletic evolution' occurring within lineages...
. In sufficiently small populations, drift can also neutralize the effect of deterministic natural selection
Natural selection
Natural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
on the population.
Stochastic drift in economics and finance
Time series variables in economics and finance — for example, stock prices, gross domestic productGross domestic product
Gross domestic product refers to the market value of all final goods and services produced within a country in a given period. GDP per capita is often considered an indicator of a country's standard of living....
, etc. — generally evolve stochastically and frequently are non-stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
. They are typically modelled as either trend stationary or difference stationary
Unit root
In time series models in econometrics , a unit root is a feature of processes that evolve through time that can cause problems in statistical inference if it is not adequately dealt with....
. A trend stationary process {yt} evolves according to
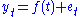
where t is time, f is a deterministic function, and et is a zero-long-run-mean stationary random variable. In this case the stochastic drift can be removed from the data by regressing
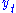on using a functional form coinciding with that of f, and retaining the residuals. In contrast, a unit root (difference stationary) process evolves according towhere
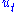is a zero-long-run-mean stationary random variable; here c is a non-stochastic drift parameter: in the absence of the random shocks ut, the mean of the process would change by c per period. In this case the non-stationarity can be removed from the data by first differencing, and the differenced variable 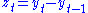will have a mean of c and hence no drift.In the context of monetary policy
Monetary policy
Monetary policy is the process by which the monetary authority of a country controls the supply of money, often targeting a rate of interest for the purpose of promoting economic growth and stability. The official goals usually include relatively stable prices and low unemployment...
, one policy question is whether a central bank should attempt to achieve a fixed growth rate of the price level
Price level
A price level is a hypothetical measure of overall prices for some set of goods and services, in a given region during a given interval, normalized relative to some base set...
from its current level in each time period, or whether to target a return of the price level to a predetermined growth path. In the latter case no price level drift is allowed away from the predetermined path, while in the former case any stochastic change to the price level permanently affects the expected values of the price level at each time along its future path. In either case the price level has drift in the sense of a rising expected value, but the cases differ according to the type of non-stationarity: difference stationarity in the former case, but trend stationarity in the latter case.
See also
- Secular variationSecular variationThe secular variation of a time series is its long-term non-periodic variation . Whether something is perceived as a secular variation or not depends on the available timescale: a secular variation over a time scale of centuries may be part of a periodic variation over a time scale of millions of...
- Decomposition of time series