Stokes relations
Encyclopedia
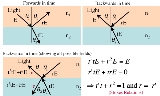
Stokes relations describe the relative phase of light reflected at a boundary between materials of different refractive index
. They also relate the transmission and reflection coefficients for the interaction. Their derivation relies on a cunning time reversal argument, so they only work when there is no absorption in the system.
You start with a reflection of the incoming field E, that is reflected and transmitted at the dielectric boundary to give rE and tE, where r and t are the amplitude reflection and transmission coefficients respectively. Next you have to realise that, since there is no absorption, this system is reversible, as shown in the second picture where the direction of the beams has been reversed. If this reversed process were actually taking place, there will be parts of the incoming fields rE and tE that are themselves transmitted and reflected at the boundary. In the third picture this is shown, where we now have coefficients r and t for reflection and transmission of the reversed fields. The only thing is that everything must interfere so that the second and third pictures agree. This means that the beam x has amplitude ‘’E” and the beam y has amplitude 0, giving Stokes relations.
The most interesting result here is that r=-r’. This means that whatever phase is associated with reflection on one side of the interface, it is 180 degrees different on the other side of the interface. For example, if , r has a phase of 0, r’ has a phase of 180 degrees.
Explicit values of the transmission and reflection coefficients are given by the Fresnel equations
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
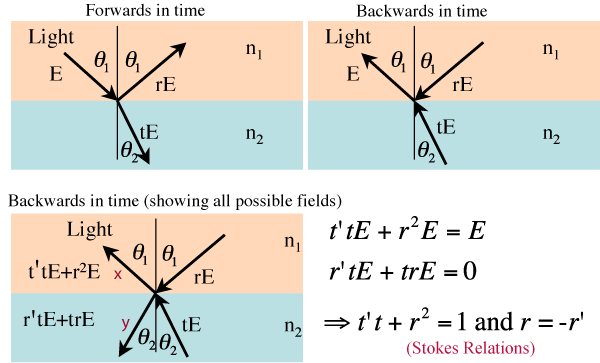
. They also relate the transmission and reflection coefficients for the interaction. Their derivation relies on a cunning time reversal argument, so they only work when there is no absorption in the system.
You start with a reflection of the incoming field E, that is reflected and transmitted at the dielectric boundary to give rE and tE, where r and t are the amplitude reflection and transmission coefficients respectively. Next you have to realise that, since there is no absorption, this system is reversible, as shown in the second picture where the direction of the beams has been reversed. If this reversed process were actually taking place, there will be parts of the incoming fields rE and tE that are themselves transmitted and reflected at the boundary. In the third picture this is shown, where we now have coefficients r and t for reflection and transmission of the reversed fields. The only thing is that everything must interfere so that the second and third pictures agree. This means that the beam x has amplitude ‘’E” and the beam y has amplitude 0, giving Stokes relations.
The most interesting result here is that r=-r’. This means that whatever phase is associated with reflection on one side of the interface, it is 180 degrees different on the other side of the interface. For example, if , r has a phase of 0, r’ has a phase of 180 degrees.
Explicit values of the transmission and reflection coefficients are given by the Fresnel equations
Fresnel equations
The Fresnel equations , deduced by Augustin-Jean Fresnel , describe the behaviour of light when moving between media of differing refractive indices...


