
Strictly singular operator
Encyclopedia
In functional analysis
, a branch of mathematics
, a strictly singular operator is a bounded linear operator L from a Banach space
X to another Banach space Y, such that it is not an isomorphism
, and fails to be an isomorphism on any infinitely dimensional subspace of X. Any compact operator
is strictly singular, but not vice-versa.
Every bounded linear map , for
, for 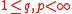 ,
,  , is strictly singular. Here,
, is strictly singular. Here, 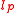 and
and  are sequence space
are sequence space
s. Similarly, every bounded linear map and
and  , for
, for 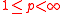 , is strictly singular. Here
, is strictly singular. Here 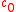 is the Banach space of sequences converging to zero. This is a corollary of Pitt's theorem, which states that such T, for q < p, are compact.
is the Banach space of sequences converging to zero. This is a corollary of Pitt's theorem, which states that such T, for q < p, are compact.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a strictly singular operator is a bounded linear operator L from a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X to another Banach space Y, such that it is not an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, and fails to be an isomorphism on any infinitely dimensional subspace of X. Any compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
is strictly singular, but not vice-versa.
Every bounded linear map
 , for
, for 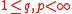 ,
,  , is strictly singular. Here,
, is strictly singular. Here, 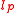 and
and  are sequence space
are sequence spaceSequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
s. Similarly, every bounded linear map
 and
and  , for
, for 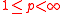 , is strictly singular. Here
, is strictly singular. Here 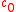 is the Banach space of sequences converging to zero. This is a corollary of Pitt's theorem, which states that such T, for q < p, are compact.
is the Banach space of sequences converging to zero. This is a corollary of Pitt's theorem, which states that such T, for q < p, are compact.

