
Strip algebra
Encyclopedia
Strip Algebra is a set of elements and operators for the description of carbon nanotube
structures, considered as a subgroup of polyhedra, and more precisely, of polyhedra with vertices
formed by three edges. This restriction is imposed on the polyhedra because carbon nanotubes are formed of sp2 carbon atoms.
s and crystal
s formed of carbon
atoms in sp2 hybridization. Thus, the atoms are arranged on a hexagonal grid. Graphite
, nanotubes, and fullerene
s are examples of graphitic systems. All of them share the property that cach atom is bonded to three others (3-valent
).
The relation between the number of vertices, edges and faces of any finite polyhedron is given by Euler's polyhedron formula
:
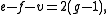
where e, f and v are the number of edges, faces and vertices, respectively, and g is the genus of the polyhedron, i.e., the number of "holes" in the surface. For example, a sphere
is a surface of genus 0, while a torus
is of genus 1.
s of the defect can be extracted from these.
Numerous complex structures can be formed with strips. As said before, strips have both at the beginning and at the end two connections. With strips only, can be formed two of them.
Carbon nanotube
Carbon nanotubes are allotropes of carbon with a cylindrical nanostructure. Nanotubes have been constructed with length-to-diameter ratio of up to 132,000,000:1, significantly larger than for any other material...
structures, considered as a subgroup of polyhedra, and more precisely, of polyhedra with vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
formed by three edges. This restriction is imposed on the polyhedra because carbon nanotubes are formed of sp2 carbon atoms.
Background
Graphitic systems are moleculeMolecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s and crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s formed of carbon
Carbon
Carbon is the chemical element with symbol C and atomic number 6. As a member of group 14 on the periodic table, it is nonmetallic and tetravalent—making four electrons available to form covalent chemical bonds...
atoms in sp2 hybridization. Thus, the atoms are arranged on a hexagonal grid. Graphite
Graphite
The mineral graphite is one of the allotropes of carbon. It was named by Abraham Gottlob Werner in 1789 from the Ancient Greek γράφω , "to draw/write", for its use in pencils, where it is commonly called lead . Unlike diamond , graphite is an electrical conductor, a semimetal...
, nanotubes, and fullerene
Fullerene
A fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
s are examples of graphitic systems. All of them share the property that cach atom is bonded to three others (3-valent
Valence (chemistry)
In chemistry, valence, also known as valency or valence number, is a measure of the number of bonds formed by an atom of a given element. "Valence" can be defined as the number of valence bonds...
).
The relation between the number of vertices, edges and faces of any finite polyhedron is given by Euler's polyhedron formula
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
:
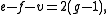
where e, f and v are the number of edges, faces and vertices, respectively, and g is the genus of the polyhedron, i.e., the number of "holes" in the surface. For example, a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is a surface of genus 0, while a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
is of genus 1.
Nomenclature
A substrip is identified by a pair of natural numbers measuring the position of the last ring in parentheses, together with the turns induced by the defect ring. The number of edgeEdge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
s of the defect can be extracted from these.
Elements
A Strip is defined as a set of consecutive rings, that is able to be joined with others, by sharing a side of the first or last ring.Numerous complex structures can be formed with strips. As said before, strips have both at the beginning and at the end two connections. With strips only, can be formed two of them.
Operators
Given the definition of a strip,- Addition of two strips: (upcoming)
- Turn Operators: (upcoming)
- Inversion of a strip: (upcoming)
Applications
- Strip Algebra has been applied to the construction of nanotube heterojunctions, and was first implemented in the CoNTub v1.0CoNTubCoNTub is software written in Java which runs on Windows, Mac OS X, Linux and Unix Operating systems. It is the first implementation of an algorithm for generating the 3D structure of two arbitrary connected carbon nanotubes by means of one defect or disclination .The software is a set of tools...
software, which makes it possible to find the precise position of all the carbon rings needed to produce a heterojunction with arbitrary indices and chirality from two nanotubeCarbon nanotubeCarbon nanotubes are allotropes of carbon with a cylindrical nanostructure. Nanotubes have been constructed with length-to-diameter ratio of up to 132,000,000:1, significantly larger than for any other material...
s.

