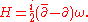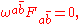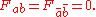Strominger's equations
Encyclopedia
In heterotic string theory
, the Strominger
's equations are the set of equations that are necessary and sufficient conditions for spacetime supersymmetry
. It is derived by requiring the 4-dimensional spacetime to be maximally symmetric, and adding a warp factor on the internal 6-dimensional manifold.
Consider a metric
on the real 6-dimensional internal manifold Y and a Hermitian metric h on a vector bundle V. The equations are:
These equations imply the usual field equations, and thus are the only equations to be solved.
However, there are topological obstructions in obtaining the solutions to the equations;
In case V is the tangent bundle
and 
is Kahler, we can obtain a solution of these equations by taking the Calabi-Yau metric on 
and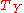 
.
Once the solutions for the Strominger's equations are obtained, the warp factor
, dilaton 
and the background flux H, are determined by
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the Strominger
Andrew Strominger
Andrew Eben Strominger is an American theoretical physicist who works on string theory and son of Jack L. Strominger. He is currently a professor at Harvard University and a senior fellow at the Society of Fellows...
's equations are the set of equations that are necessary and sufficient conditions for spacetime supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. It is derived by requiring the 4-dimensional spacetime to be maximally symmetric, and adding a warp factor on the internal 6-dimensional manifold.
Consider a metric
on the real 6-dimensional internal manifold Y and a Hermitian metric h on a vector bundle V. The equations are:- The 4-dimensional spacetime is MinkowskiMinkowskiMinkowski is a surname, and may refer to:* Eugène Minkowski , French psychiatrist* Hermann Minkowski Russian-born German mathematician and physicist, known for:** Minkowski addition** Minkowski–Bouligand dimension...
, i.e.,
. - The internal manifold Y must be complex, i.e., the Nijenhuis tensor must vanish
. - The Hermitian form
on the complex threefold Y, and the Hermitian metric h on a vector bundle V must satisfy,
-
-
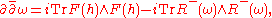
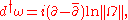
where
is the Hull-curvature two-form of 
, F is the curvature of h, and 
is the holomorphic n-form; F is also known in the physics literature as the Yang-Mills field strength. Li and Yau showed that the second condition is equivalent to 
being conformally balanced, i.e.,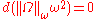 
.
-
- The Yang-Mills field strength must satisfy,
-
These equations imply the usual field equations, and thus are the only equations to be solved.
However, there are topological obstructions in obtaining the solutions to the equations;
- The second Chern classChern classIn mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the manifold, and the second Chern class of the gauge field must be equal, i.e.,
- A holomorphic n-form
must exists, i.e., 
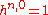and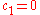 
.
In case V is the tangent bundle
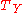and is Kahler, we can obtain a solution of these equations by taking the Calabi-Yau metric on and 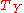.Once the solutions for the Strominger's equations are obtained, the warp factor
, dilaton and the background flux H, are determined by
-
, -
, -
