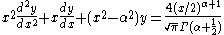Struve function
Encyclopedia
In mathematics
, Struve functions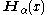 , are solutions y(x) of the non-homogenous Bessel's differential equation:
, are solutions y(x) of the non-homogenous Bessel's differential equation:
introduced by .
The complex number
α is the order of the Struve function, and is often an integer.
The modified Struve functions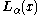 are equal to
are equal to
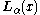 .
.
solutions can be constructed from a single particular solution by adding the solutions of the homogeneous problem.
In this case, the homogenous solutions are the Bessel function
s, and the particular solution may be chosen as the corresponding Struve function.
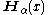 have the following power series form
have the following power series form
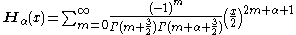
where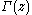 is the gamma function
is the gamma function
.
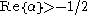 , is possible using an integral representation:
, is possible using an integral representation:
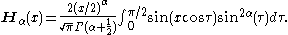
For large x, one obtains:
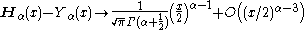
where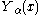 is the
is the
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Struve functions
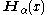 , are solutions y(x) of the non-homogenous Bessel's differential equation:
, are solutions y(x) of the non-homogenous Bessel's differential equation:introduced by .
The complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
α is the order of the Struve function, and is often an integer.
The modified Struve functions
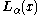 are equal to
are equal to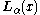 .
.Definitions
Since this is a non-homogenous equation,solutions can be constructed from a single particular solution by adding the solutions of the homogeneous problem.
In this case, the homogenous solutions are the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s, and the particular solution may be chosen as the corresponding Struve function.
Power series expansion
Struve functions, denoted as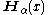 have the following power series form
have the following power series form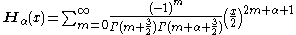
where
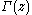 is the gamma function
is the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
Integral form
Another definition of the Struve function, for values of α satisfying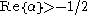 , is possible using an integral representation:
, is possible using an integral representation: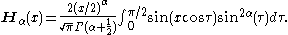
Asymptotic forms
For small x, the power series expansion is given above.For large x, one obtains:
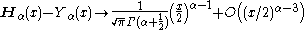
where
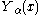 is the
is the