
Subspace theorem
Encyclopedia
In mathematics, the subspace theorem is a result obtained by . It states that if L1,...,Ln are linearly independent
linear
forms in n variables with algebraic
coefficients and if ε>0 is any given real number, then
the non-zero integer points x with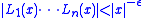
lie in a finite number of proper subspaces
of Qn.
Schmidt's subspace theorem was generalised in by Schlickewei (1977) to allow more general absolute values
.
If a1,...,an are algebraic such that 1,a1,...,an are linearly independent over Q and ε>0 is any given real number, then there are only finitely many rational n-tuples (x1/y,...,xn/y) with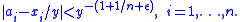
The specialization n = 1 gives the Thue–Siegel–Roth theorem
. One may also note that the exponent 1+1/n+ε is best possible by Dirichlet's theorem on diophantine approximation.
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
forms in n variables with algebraic
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
coefficients and if ε>0 is any given real number, then
the non-zero integer points x with
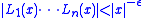
lie in a finite number of proper subspaces
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of Qn.
Schmidt's subspace theorem was generalised in by Schlickewei (1977) to allow more general absolute values
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
.
A corollary on Diophantine approximation
The following corollary to the subspace theorem is often itself referred to as the subspace theorem.If a1,...,an are algebraic such that 1,a1,...,an are linearly independent over Q and ε>0 is any given real number, then there are only finitely many rational n-tuples (x1/y,...,xn/y) with
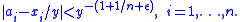
The specialization n = 1 gives the Thue–Siegel–Roth theorem
Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
. One may also note that the exponent 1+1/n+ε is best possible by Dirichlet's theorem on diophantine approximation.

