Sullivan conjecture
Encyclopedia
In mathematics
, Sullivan conjecture can refer to any of several results and conjectures prompted by homotopy theory work of Dennis Sullivan
. A basic theme and motivation concerns the fixed point
set in group action
s of a finite group
. The most elementary formulation, however, is in terms of the classifying space
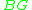of such a group. Roughly speaking, it is difficult to map such a space 
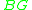continuously into a finite CW complex
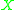. Such a version of the Sullivan conjecture was first proved by Haynes Miller.
In 1984, Miller proved that the function space
, carrying the compact-open topology
, of base point-preserving mappings from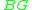
to 
is then weakly contractible
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Sullivan conjecture can refer to any of several results and conjectures prompted by homotopy theory work of Dennis Sullivan
Dennis Sullivan
Dennis Parnell Sullivan is an American mathematician. He is known for work in topology, both algebraic and geometric, and on dynamical systems. He holds the Albert Einstein Chair at the City University of New York Graduate Center, and is a professor at Stony Brook University.-Work in topology:He...
. A basic theme and motivation concerns the fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
set in group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
. The most elementary formulation, however, is in terms of the classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
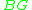of such a group. Roughly speaking, it is difficult to map such a space 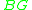continuously into a finite CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
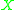. Such a version of the Sullivan conjecture was first proved by Haynes Miller.In 1984, Miller proved that the function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
, carrying the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
, of base point-preserving mappings from
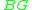to is then weakly contractibleWeakly contractible
In mathematics, a topological space is said to be weakly contractible if all of its homotopy groups are trivial.-Property:It follows from Whitehead's Theorem that if a CW-complex is weakly contractible then it is contractible.-Example:...
.