Sum-product number
Encyclopedia
A sum-product number is an integer that in a given base is equal to the sum of its digits times the product of its digits. Or, to put it algebraically, given an integer n that is l digits long in base b (with dx representing the xth digit), if
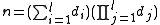
then n is a sum-product number in base b. In base 10, the only sum-product numbers are 0
, 1, 135
, 144
. Thus, for example, 144 is a sum-product number because 1 + 4 + 4 = 9, and 1 × 4 × 4 = 16, and 9 × 16 = 144.
1 is a sum-product number in any base, because of the multiplicative identity. 0 is also a sum-product number in any base, but no other integer with significant zeroes in the given base can be a sum-product number. 0 and 1 are also unique in being the only single-digit sum-product numbers in any given base; for any other single-digit number, the sum of the digits times the product of the digits works out to the number itself squared.
Any integer shown to be a sum-product number in a given base must, by definition, also be a Harshad number
in that base.
In binary
, 0 and 1 are the only sum-product numbers. The following table lists some sum-product numbers in a few selected bases:
The finiteness of the list for base 10
was proven by David Wilson. First he proved that a base 10 sum-product number will not have more than 84 digits. Next, he ruled out numbers with significant zeroes. Thereafter he concentrated on digit products of the forms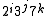
or 
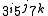, which the previous constraints reduce to a set small enough to be testable by brute force in a reasonable period of time.
From Wilson's proof, Raymond Puzio developed the proof that in any positional base system there is only a finite set of sum-product numbers. First he proved that
. Since the largest digit in the base represents b - 1, the maximum possible value of the sum of digits of n is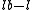 
and the maximum possible value of the product of digits is 
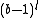. Multiplying the maximum possible sum by the maximum possible product gives 
. From this, Puzio deduced that because of the growth of the exponential function, 
can be true only for l less than the limit.
In Roman numerals, the only sum-product numbers are 1, 2, 3, and possibly 4 (if written IIII).
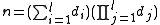
then n is a sum-product number in base b. In base 10, the only sum-product numbers are 0
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, 1, 135
135 (number)
135 is the natural number following 134 and preceding 136.-In mathematics:This number in base 10 can be expressed in operations using its own digits in at least two different ways...
, 144
144 (number)
144 is the natural number following 143 and preceding 145. 144 is a dozen dozens, or one gross.-In mathematics:It is the twelfth Fibonacci number, and the largest one to also be a square, as the square of 12 , following 89 and preceding 233.144 is the smallest number with exactly 15 divisors.144 is...
. Thus, for example, 144 is a sum-product number because 1 + 4 + 4 = 9, and 1 × 4 × 4 = 16, and 9 × 16 = 144.
1 is a sum-product number in any base, because of the multiplicative identity. 0 is also a sum-product number in any base, but no other integer with significant zeroes in the given base can be a sum-product number. 0 and 1 are also unique in being the only single-digit sum-product numbers in any given base; for any other single-digit number, the sum of the digits times the product of the digits works out to the number itself squared.
Any integer shown to be a sum-product number in a given base must, by definition, also be a Harshad number
Harshad number
A Harshad number, or Niven number in a given number base, is an integer that is divisible by the sum of its digits when written in that base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "Harshad" comes from the Sanskrit + , meaning joy-giver. The Niven...
in that base.
In binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
, 0 and 1 are the only sum-product numbers. The following table lists some sum-product numbers in a few selected bases:
| Base | Sum-product numbers | Values in base 10 |
|---|---|---|
| 4 | 0, 1, 12 | 0, 1, 6 |
| 5 | 0, 1, 341 | 0, 1, 96 |
| 7 | 0, 1, 22, 242, 1254, 2343 | 0, 1, 16, 128, 480, 864 |
| 9 | 0, 1, 13 | 0, 1, 12 |
| 10 | 0, 1, 135, 144 | 0, 1, 135, 144 |
| 12 | 0, 1, 128, 173, 353 | 0, 1, 176, 231, 495 |
| 36 | 0, 1, 16, 22O | 0, 1, 42, 2688 |
The finiteness of the list for base 10
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
was proven by David Wilson. First he proved that a base 10 sum-product number will not have more than 84 digits. Next, he ruled out numbers with significant zeroes. Thereafter he concentrated on digit products of the forms
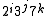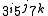or , which the previous constraints reduce to a set small enough to be testable by brute force in a reasonable period of time.From Wilson's proof, Raymond Puzio developed the proof that in any positional base system there is only a finite set of sum-product numbers. First he proved that
. Since the largest digit in the base represents b - 1, the maximum possible value of the sum of digits of n is 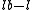and the maximum possible value of the product of digits is 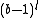. Multiplying the maximum possible sum by the maximum possible product gives . From this, Puzio deduced that because of the growth of the exponential function, can be true only for l less than the limit.In Roman numerals, the only sum-product numbers are 1, 2, 3, and possibly 4 (if written IIII).