
Supercommutative algebra
Encyclopedia
In mathematics
, a supercommutative algebra is a superalgebra
(i.e. a Z2-graded algebra
) such that for any two homogeneous elements x, y we have
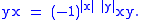
Equivalently, it is a superalgebra where the supercommutator

always vanishes. Algebraic structures which supercommute in the above sense are sometimes referred to as skew-commutative associative algebras to emphasize the anti-commutation, or, to emphasize the grading, graded-commutative or, if the supercommutativity is understood, simply commutative.
Any commutative algebra
is a supercommutative algebra if given the trivial gradation (i.e. all elements are even). Grassmann algebras (also known as exterior algebra
s) are the most common examples of nontrivial supercommutative algebras. The supercenter of any superalgebra is the set of elements that supercommute with all elements, and is a supercommutative algebra.
The even subalgebra of a supercommutative algebra is always a commutative algebra
. That is, even elements always commute. Odd elements, on the other hand, always anticommute. That is,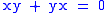
for odd x and y. In particular, the square of any odd element x vanishes whenever 2 is invertible:
Thus a commutative superalgebra (with 2 invertible and nonzero degree one component) always contains nilpotent
elements.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a supercommutative algebra is a superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
(i.e. a Z2-graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
) such that for any two homogeneous elements x, y we have
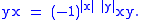
Equivalently, it is a superalgebra where the supercommutator

always vanishes. Algebraic structures which supercommute in the above sense are sometimes referred to as skew-commutative associative algebras to emphasize the anti-commutation, or, to emphasize the grading, graded-commutative or, if the supercommutativity is understood, simply commutative.
Any commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
is a supercommutative algebra if given the trivial gradation (i.e. all elements are even). Grassmann algebras (also known as exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
s) are the most common examples of nontrivial supercommutative algebras. The supercenter of any superalgebra is the set of elements that supercommute with all elements, and is a supercommutative algebra.
The even subalgebra of a supercommutative algebra is always a commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
. That is, even elements always commute. Odd elements, on the other hand, always anticommute. That is,
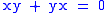
for odd x and y. In particular, the square of any odd element x vanishes whenever 2 is invertible:

Thus a commutative superalgebra (with 2 invertible and nonzero degree one component) always contains nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
elements.

