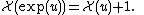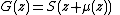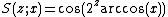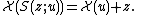Superfunction
Encyclopedia
In mathematics, a superfunction is a nonstandard name for an iterated function
for complexified continuous iteration index.
Roughly, for some function f and for some variable x, the superfunction could be defined by the expression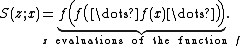
Then, S(z;x) can be interpreted as the superfunction of the function f(x).
Such a definition is valid only for a positive integer index z. The variable x is often omitted.
Much study and many applications of superfunctions employ various extensions of these superfunctions to complex and continuous indices; and the analysis of the existence, uniqueness and their evaluation. The Ackermann function
s and tetration
can be interpreted in terms of super-functions.
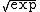 ; the function
; the function 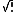 has then been used as the logo of the Physics department of the Moscow State University
has then been used as the logo of the Physics department of the Moscow State University
.
At that time, these investigators did not have computational access for the evaluation of such functions, but the function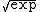 was luckier than
was luckier than  : at the very least, the existence of the holomorphic function
: at the very least, the existence of the holomorphic function
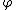 such that
such that  had been demonstrated in 1950 by Helmuth Kneser.
had been demonstrated in 1950 by Helmuth Kneser.
Relying on the elegant functional conjugacy theory of Schröder's equation, for his proof, Kneser had constructed the "superfunction" of the exponential map through the corresponding Abel function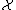 , satisfying the related Abel equation
, satisfying the related Abel equation
so that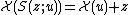 . The inverse function Kneser found,
. The inverse function Kneser found,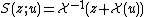
is an entire
super-exponential, although it is not real on the real axis; it cannot be interpreted as tetration
al, because the condition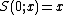 cannot be realized for the entire super-exponential. The real
cannot be realized for the entire super-exponential. The real 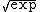 can be constructed with the tetration
can be constructed with the tetration
al (which is also a superexponential); while the real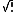 can be constructed with the superfactorial.
can be constructed with the superfactorial.
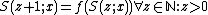
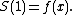
Instead of the last equation, one could write the identity function,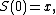
and extend the range of definition of the superfunction S to the non-negative integers. Then, one may posit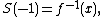
and extend the range of validity to the integer values larger than −2.
The following extension, for example,
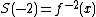
is not trivial, because the inverse function may happen to be not defined for some values of .
.
In particular, tetration
can be interpreted as super-function of exponential for some real base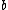 ; in this case,
; in this case,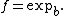
Then, at x=1,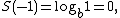
but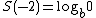
is not defined.
For extension to non-integer values of the argument, the superfunction should be defined in a different way.
For complex numbers and
and  , such that
, such that  belongs to some connected domain
belongs to some connected domain 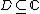 ,
,
the superfunction (from to
to 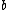 ) of a holomorphic function
) of a holomorphic function
f on the domain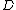 is
is
function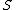 , holomorphic on domain
, holomorphic on domain 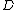 , such that
, such that
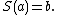
For a given base function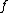 , from a given
, from a given 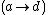 superfunction
superfunction 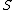 , another
, another 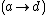 superfunction
superfunction 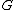 could be constructed as
could be constructed as
where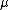 is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that
is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that  .
.
The modified super-function may have a narrower range of holomorphy.
The variety of possible super-functions is especially large in the limiting case, when the width of the range of holomorphy becomes zero; in this case, one deals with real-analytic superfunctions.
If the range of holomorphy required is large enough, then, the super-function is expected to be unique,
at least in some specific base functions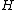 . In particular, the
. In particular, the 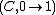 super-function of
super-function of
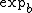 , for
, for 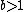 , is called tetration
, is called tetration
and is believed to be unique, at least for
 ; for the case
; for the case  ,
,
but up to 2009, the uniqueness was more conjecture
than a theorem with a formal mathematical proof.
they are used without mention that they are superfunctions.
For example, for the transfer function "++", which means unity increment,
the superfunction is just addition of a constant.
 and define the function
and define the function 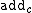 as
as
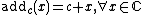 . Further define the function
. Further define the function 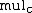 as
as
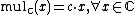 .
.
Then, the function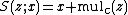 is the superfunction (0 to c)
is the superfunction (0 to c)
of the function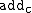 on C.
on C.
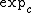 is superfunction (from 1 to
is superfunction (from 1 to  ) of function
) of function 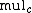 .
.
Let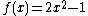 .
.
Then,
is a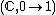 superfunction (iteration orbit) of f.
superfunction (iteration orbit) of f.
Indeed,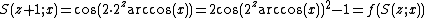
and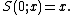
In this case, the superfunction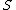 is periodic, with period
is periodic, with period
 ;
;
and the superfunction approaches unity in the negative direction of the real axis,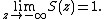
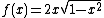
iterates to an orbit
. An example involving a meromorphic function
f reads,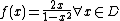 ;
; 
Its iteration orbit (superfunction) is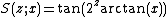
on C, the set of complex numbers except for the singularities of the function S.
To see this, recall the double angle trigonometric formula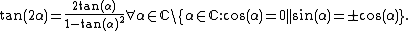
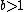 ,
,
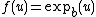 ,
,
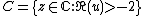 .
.
The tetration
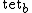 is then a
is then a  superfunction of
superfunction of 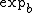 .
.
, the solution of the Abel equation
,
and hence
The inverse function when defined, is
for suitable domains and ranges, when they exist. The recursive property of S is then self-evident.
The figure at left shows an example of transition from
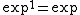 to
to
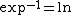 .
.
The iterated function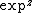 versus real argument is plotted for
versus real argument is plotted for
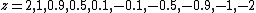 . The tetration
. The tetration
al and ArcTetrational were used as superfunction
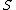 and Abel function
and Abel function 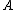 of the exponential.
of the exponential.
The figure at right shows these functions in the complex plane.
At non-negative integer number of iteration, the iterated exponential is an entire function
; at non-integer values, it has two branch points, thich correspond to the fixed point
 and
and
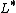 of natural logarithm. At
of natural logarithm. At 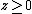 , function
, function  remains holomorphic
remains holomorphic
at least in the strip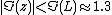 along the real axis.
along the real axis.
s, are proposed as a fast-growing function for an
upgrade of the floating point
representation of numbers in computers. Such an upgrade would greatly extend the
range of huge numbers which are still distinguishable from infinity.
Other applications refer to the calculation of fractional iterates
(or fractional power) of a function. Any holomorphic function can be declared as a "transfer function", then its superfunctions and
corresponding Abel functions can be considered.
Similar example is suggested for a nonlinear optical fiber.
as it diffuses down through a tube with some uniform concentration of vapor.
In the first approximation, at fixed concentration of the vapor,
the mass of the drop at the output end can be interpreted as the
Transfer Function of the input mass.
The square root of this Transfer Function will characterize the tube of half length.
(that can be determined by the altitude of the hill) this mass can be considered also as a Transfer Function of the input mass. The mass of the snowball could be measured at the top of the hill and at the bottom, giving the Transfer Function; then, the mass of the snowball, as a function of the length it passed, is a superfunction.
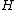 ,
,
and wants to realize it as a sequential connection of a couple of identical operational elements, then, each of these two elements should have transfer function
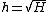 . Such a function can be evaluated through the superfunction and the Abel function of the transfer function
. Such a function can be evaluated through the superfunction and the Abel function of the transfer function 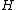 .
.
The operational element may have any origin: it can be realized as an electronic microchip,
or a mechanical couple of curvilinear grains, or some asymmetric U-tube filled with different liquids, and so on.
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
for complexified continuous iteration index.
Roughly, for some function f and for some variable x, the superfunction could be defined by the expression
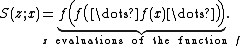
Then, S(z;x) can be interpreted as the superfunction of the function f(x).
Such a definition is valid only for a positive integer index z. The variable x is often omitted.
Much study and many applications of superfunctions employ various extensions of these superfunctions to complex and continuous indices; and the analysis of the existence, uniqueness and their evaluation. The Ackermann function
Ackermann function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
s and tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
can be interpreted in terms of super-functions.
History
Analysis of superfunctions arose from applications of the evaluation of fractional iterations of functions. Superfunctions and their inverses allow evaluation of not only the first negative power of a function (inverse function), but also of any real and even complex iterate of that function. Historically, an early function of this kind considered was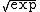 ; the function
; the function 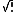 has then been used as the logo of the Physics department of the Moscow State University
has then been used as the logo of the Physics department of the Moscow State UniversityMoscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
.
At that time, these investigators did not have computational access for the evaluation of such functions, but the function
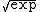 was luckier than
was luckier than  : at the very least, the existence of the holomorphic function
: at the very least, the existence of the holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
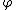 such that
such that  had been demonstrated in 1950 by Helmuth Kneser.
had been demonstrated in 1950 by Helmuth Kneser.Relying on the elegant functional conjugacy theory of Schröder's equation, for his proof, Kneser had constructed the "superfunction" of the exponential map through the corresponding Abel function
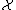 , satisfying the related Abel equation
, satisfying the related Abel equationAbel equation
The Abel equation, named after Niels Henrik Abel, is special case of functional equations which can be written in the formf = h\,\!or\alpha=\alpha+1\!and shows non-trivial properties at the iteration.-Equivalence:...
so that
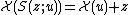 . The inverse function Kneser found,
. The inverse function Kneser found,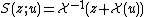
is an entire
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
super-exponential, although it is not real on the real axis; it cannot be interpreted as tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
al, because the condition
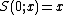 cannot be realized for the entire super-exponential. The real
cannot be realized for the entire super-exponential. The real 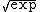 can be constructed with the tetration
can be constructed with the tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
al (which is also a superexponential); while the real
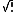 can be constructed with the superfactorial.
can be constructed with the superfactorial.Extensions
The recurrence formula of the above preamble can be written as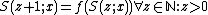
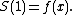
Instead of the last equation, one could write the identity function,
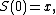
and extend the range of definition of the superfunction S to the non-negative integers. Then, one may posit
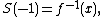
and extend the range of validity to the integer values larger than −2.
The following extension, for example,
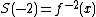
is not trivial, because the inverse function may happen to be not defined for some values of
 .
.In particular, tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
can be interpreted as super-function of exponential for some real base
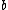 ; in this case,
; in this case,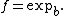
Then, at x=1,
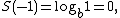
but
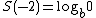
is not defined.
For extension to non-integer values of the argument, the superfunction should be defined in a different way.
For complex numbers
 and
and  , such that
, such that  belongs to some connected domain
belongs to some connected domain 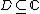 ,
,the superfunction (from
 to
to 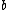 ) of a holomorphic function
) of a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
f on the domain
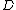 is
isfunction
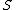 , holomorphic on domain
, holomorphic on domain 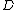 , such that
, such that
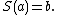
Uniqueness
In general, the superfunction is not unique.For a given base function
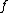 , from a given
, from a given 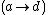 superfunction
superfunction 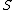 , another
, another 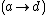 superfunction
superfunction 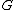 could be constructed as
could be constructed as
where
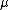 is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that
is any 1-periodic function, holomorphic at least in some vicinity of the real axis, such that  .
.The modified super-function may have a narrower range of holomorphy.
The variety of possible super-functions is especially large in the limiting case, when the width of the range of holomorphy becomes zero; in this case, one deals with real-analytic superfunctions.
If the range of holomorphy required is large enough, then, the super-function is expected to be unique,
at least in some specific base functions
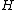 . In particular, the
. In particular, the 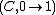 super-function of
super-function of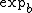 , for
, for 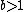 , is called tetration
, is called tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
and is believed to be unique, at least for
 ; for the case
; for the case  ,
,but up to 2009, the uniqueness was more conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
than a theorem with a formal mathematical proof.
Examples
This short collection of elementary superfunctions is illustrated in. Some superfunctions can be expressed through elementary functions;they are used without mention that they are superfunctions.
For example, for the transfer function "++", which means unity increment,
the superfunction is just addition of a constant.
Addition
Chose a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
 and define the function
and define the function 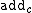 as
as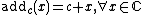 . Further define the function
. Further define the function 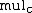 as
as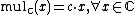 .
.Then, the function
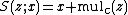 is the superfunction (0 to c)
is the superfunction (0 to c)of the function
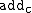 on C.
on C.Multiplication
Exponentiation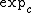 is superfunction (from 1 to
is superfunction (from 1 to  ) of function
) of function 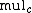 .
.Quadratic polynomials
The examples but the last one, below, are essentially from Schröder's pioneering 1870 paper.Let
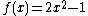 .
.Then,
is a
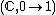 superfunction (iteration orbit) of f.
superfunction (iteration orbit) of f.Indeed,
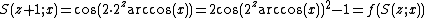
and
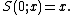
In this case, the superfunction
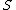 is periodic, with period
is periodic, with period ;
;and the superfunction approaches unity in the negative direction of the real axis,
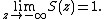
Algebraic function
Similarly,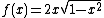
iterates to an orbit

Rational function
In general, the transfer (step) function f(x) needs not be an entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
. An example involving a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
f reads,
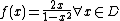 ;
; 
Its iteration orbit (superfunction) is
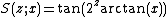
on C, the set of complex numbers except for the singularities of the function S.
To see this, recall the double angle trigonometric formula
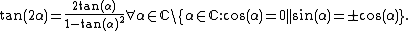
Exponentiation
Let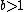 ,
,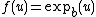 ,
,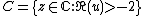 .
.The tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
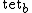 is then a
is then a  superfunction of
superfunction of 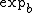 .
.Abel functions (under deconstruction)
The inverse of a superfunction for a suitable argument x can be interpreted as the Abel functionAbel function
In mathematics Abel function is a special kind of solution of the Abel equations, used to classify them as superfunctions, and formulate conditions of uniqueness.The Abel equation is class of equations which can be written in the formg=g+1...
, the solution of the Abel equation
Abel equation
The Abel equation, named after Niels Henrik Abel, is special case of functional equations which can be written in the formf = h\,\!or\alpha=\alpha+1\!and shows non-trivial properties at the iteration.-Equivalence:...
,
and hence
The inverse function when defined, is

for suitable domains and ranges, when they exist. The recursive property of S is then self-evident.
The figure at left shows an example of transition from
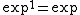 to
to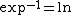 .
.The iterated function
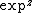 versus real argument is plotted for
versus real argument is plotted for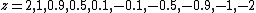 . The tetration
. The tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
al and ArcTetrational were used as superfunction
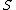 and Abel function
and Abel function 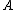 of the exponential.
of the exponential.The figure at right shows these functions in the complex plane.
At non-negative integer number of iteration, the iterated exponential is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
; at non-integer values, it has two branch points, thich correspond to the fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
 and
and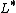 of natural logarithm. At
of natural logarithm. At 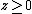 , function
, function  remains holomorphic
remains holomorphicHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
at least in the strip
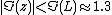 along the real axis.
along the real axis.Applications of superfunctions and Abel functions
Superfunctions, usually the superexponentialTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
s, are proposed as a fast-growing function for an
upgrade of the floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
representation of numbers in computers. Such an upgrade would greatly extend the
range of huge numbers which are still distinguishable from infinity.
Other applications refer to the calculation of fractional iterates
(or fractional power) of a function. Any holomorphic function can be declared as a "transfer function", then its superfunctions and
corresponding Abel functions can be considered.
Nonlinear optics
In the investigation of the nonlinear response of optical materials, the sample is supposed to be optically thin, in such a way, that the intensity of the light does not change much as it goes through. Then one can consider, for example, the absorption as function of the intensity. However, at small variation of the intensity in the sample, the precision of measurement of the absorption as function of intensity is not good. The reconstruction of the superfunction from the transfer function allows to work with relatively thick samples, improving the precision of measurements. In particular, the transfer function of the similar sample, which is half thiner, could be interpreted as the square root (i.e. half-iteration) of the transfer function of the initial sample.Similar example is suggested for a nonlinear optical fiber.
Nonlinear acoustics
It may make sense to characterize the nonlinearities in the attenuation of shock waves in a homogeneous tube. This could find an application in some advanced muffler, using nonlinear acoustic effects to withdraw the energy of the sound waves without to disturb the flux of the gas. Again, the analysis of the nonlinear response, i.e. the transfer function, may be boosted with the superfunction.Evaporation and condensation
In analysis of condensation, the growth (or vaporization) of a small drop of liquid can be considered,as it diffuses down through a tube with some uniform concentration of vapor.
In the first approximation, at fixed concentration of the vapor,
the mass of the drop at the output end can be interpreted as the
Transfer Function of the input mass.
The square root of this Transfer Function will characterize the tube of half length.
Snow avalanche
The mass of a snowball that rolls down a hill can be considered as a function of the path it has already passed. At fixed length of this path(that can be determined by the altitude of the hill) this mass can be considered also as a Transfer Function of the input mass. The mass of the snowball could be measured at the top of the hill and at the bottom, giving the Transfer Function; then, the mass of the snowball, as a function of the length it passed, is a superfunction.
Operational element
If one needs to build-up an operational element with some given transfer function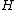 ,
,and wants to realize it as a sequential connection of a couple of identical operational elements, then, each of these two elements should have transfer function
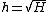 . Such a function can be evaluated through the superfunction and the Abel function of the transfer function
. Such a function can be evaluated through the superfunction and the Abel function of the transfer function 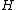 .
.The operational element may have any origin: it can be realized as an electronic microchip,
or a mechanical couple of curvilinear grains, or some asymmetric U-tube filled with different liquids, and so on.