
Superhedging price
Encyclopedia
The superhedging price is a coherent risk measure
. The superhedging price of a portfolio (A) is equivalent to the smallest amount necessary to be paid for a portfolio (B) at the current time so that at some specified future time the value of B is at least as great as A. In a complete market
the superhedging price is equivalent to the price for hedging the initial portfolio.
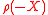 where
where  is defined by
is defined by
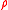 defined as above is a coherent risk measure.
defined as above is a coherent risk measure.
for the superhedging price is the negative of the set of values of a self-financing portfolio
at the terminal time. That is
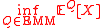 . It is obvious to see that this is the negative of the superhedging price of the negative of the initial claim (
. It is obvious to see that this is the negative of the superhedging price of the negative of the initial claim (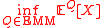 ). In a complete market then the supremum
). In a complete market then the supremum
and infimum
are equal to each other and a unique hedging price exists. The upper and lower bounds created by the subhedging and superhedging prices respectively are the no-arbitrage bounds
, an example of good-deal bounds.

It is a widely shown result that this is time consistent.
Coherent risk measure
In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have...
. The superhedging price of a portfolio (A) is equivalent to the smallest amount necessary to be paid for a portfolio (B) at the current time so that at some specified future time the value of B is at least as great as A. In a complete market
Complete market
In economics, a complete market is one in which the complete set of possible gambles on future states-of-the-world can be constructed with existing assets without friction. Every agent is able to exchange every good, directly or indirectly, with every other agent without transaction costs...
the superhedging price is equivalent to the price for hedging the initial portfolio.
Mathematical definition
If the set of equivalent martingale measures is denoted by EMM then the superhedging price of a portfolio X is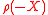 where
where  is defined by
is defined by
-
 .
.
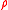 defined as above is a coherent risk measure.
defined as above is a coherent risk measure.Acceptance set
The acceptance setAcceptance set
In financial mathematics, acceptance sets are a mathematical concept related to risk measures. As the name suggests an acceptance set is a set of acceptable future net worth, which are acceptable to the regulator.-Mathematical Definition:...
for the superhedging price is the negative of the set of values of a self-financing portfolio
Self-financing portfolio
Self-financing portfolio, an important concept in financial mathematics.A portfolio is self-financing if there is no exogenous infusion or withdrawal of money; the purchase of a new asset must be financed by the sale of an old one.- Mathematical definition :...
at the terminal time. That is
-
 .
.
Subhedging price
The subhedging price is the greatest value that can be paid so that in any possible situation at the specified future time you have a second portfolio worth less or equal to the initial one. Mathematically it can be written as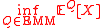 . It is obvious to see that this is the negative of the superhedging price of the negative of the initial claim (
. It is obvious to see that this is the negative of the superhedging price of the negative of the initial claim (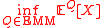 ). In a complete market then the supremum
). In a complete market then the supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
and infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
are equal to each other and a unique hedging price exists. The upper and lower bounds created by the subhedging and superhedging prices respectively are the no-arbitrage bounds
No-arbitrage bounds
In financial mathematics, no-arbitrage bounds are mathematical relationships specifying limits on financial portfolio prices. These price bounds are a specific example of good-deal bounds, and are in fact the greatest extremes for good-deal bounds....
, an example of good-deal bounds.
Dynamic superhedging price
The dynamic superhedging price has conditional risk measures of the form:
It is a widely shown result that this is time consistent.

