
Swift-Hohenberg equation
Encyclopedia
The Swift–Hohenberg equation (named after Jack B. Swift and Pierre Hohenberg
) is a partial differential equation
noted for its pattern-forming behaviour. It takes the form
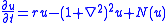
where u = u(x, t) or u = u(x, y, t) is a scalar function defined on the line or the plane, r is a real bifurcation parameter, and N(u) is some smooth nonlinearity.
The equation is named after the authors of the paper, where it was derived from the equations for thermal convection
.
The webpage of Michael Cross contains some numerical integrators which demonstrate the behaviour of several Swift–Hohenberg-like systems.
Pierre Hohenberg
Pierre C. Hohenberg is a French-American theoretical physicist, who works primarily on statistical mechanics....
) is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
noted for its pattern-forming behaviour. It takes the form
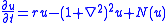
where u = u(x, t) or u = u(x, y, t) is a scalar function defined on the line or the plane, r is a real bifurcation parameter, and N(u) is some smooth nonlinearity.
The equation is named after the authors of the paper, where it was derived from the equations for thermal convection
Convection
Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids....
.
The webpage of Michael Cross contains some numerical integrators which demonstrate the behaviour of several Swift–Hohenberg-like systems.

